В задачах искусственного интеллекта.
При создании СИИ используются главным образом три раздела математики: ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ, ПРЕДИКАТЫ и НЕЧЕТКИЕ МНОЖЕСТВА. С помощью исчисления выск5азываний и теории предикатов обычные предложения на русском языке можно записать в компактной математической форме. Теория нечетких множеств позволяет решать задачи, когда мы не можем провести точное решение.
2.1. Логика высказываний.
В предыдущей главе показано, что рассуждения агента (поиск решений задачи) сводится к определению правил перехода в соответствии с выбранной стратегией. Каждый шаг состоит в проверке агентом истинности левой части правила (факта нахождения среды в состоянии bi и допустимости действия сj) и, в случае ее истинности, признании факта перехода из состояния bi в состояние bk в результате действия сj. Естественно, нам хотелось бы иметь математический аппарат, на основе которого можно осуществлять постановку и поиск решения задачи формально, используя наилучшую стратегию поиска. Логика высказываний – это первый шаг к созданию такого аппарата.
Осуществить постановку задачи формально – значит, имея некий формальный язык, выразить на нем все знания о среде, необходимые для решения задачи. Формальный язык в соответствии с современными представлениями требует рассмотрения двух его неотъемлемых частей: синтаксиса и семантики. Синтаксис языка описывает допустимые в языке предложения, состоящие из цепочек (последовательностей) символов, принадлежащих определенному множеству, называемому алфавитом. Синтаксис языка позволяет отличать предложения, принадлежащие языку, от предложений, ему не принадлежащих. Семантика языка определяет смысл этих предложений, сопоставляя символы языка с объектами реального мира, а предложения-отношения между объектами. Без семантики предложения языка являются ничего не значащими для агента цепочками символов. Семантика логики высказываний позволяет подразделять все множество допустимых предложений на истинные и ложные. Истинные – это те предложения, которые соответствуют имеющим место фактам или отношениям, а ложные – не имеющим. Решать задачу формально – значит иметь множество правил и стратегию их использования, которые позволяют осуществить вывод одних синтаксически правильных истинных предложений из других синтаксически правильных истинных или предполагаемых истинными.
Исчисление высказываний (другие названия – алгебра логики, двоичная алгебра, алгебра Буля) рассматривает операции над переменными, которые могут принимать только два значения: 0 и 1. Алгебра логики позволяет формализовать (записывать в виде формул) логические рассуждения. В этих рассуждениях оперируют понятиями истина и ложь. Понятие истина при этом обозначается 1, ложь – 0.
Функции алгебры логики – двоичные функции удобно формировать и исследовать с помощью специальных таблиц – таблиц истинности, в которых перечисляются все возможные значения одного или нескольких переменных. В таблице 2.1 представлены все возможные двоичные функции одной переменной.
| Таблица 2.1. | ||||
| Значения аргумента X | Функции | |||
| Y=0 | Y=X | Y=`X=–X |  Y=1 Y=1
| |
Первая и последняя функции являются константами, вторая – повторяет x, а вот третья, значения которой противоположны значениям х, широко используется в алгебре логики и называется отрицанием х , или инверсией, или просто функцией НЕ х. Других, кроме перечисленных функций одной переменной в алгебре логики не существует.
Функций двух переменных имеется 16, некоторые, наиболее часто используемые, приведены в таблице истинности 2.2.
Первая из этих функций называется логическим сложением или ДИЗЪЮНКЦИЕЙ или просто функцией ИЛИ. Часто её обозначают знаком +.
Вторая функция – логическое умножение или конъюнкция или функция И. Её часто обозначают знаком умножения – точкой.
Третья, четвертая и пятая функции называются, соответственно импликацией, сложением по модулю 2 и эквивалентностью.
| Таблица 2.2 | ||||||
| Значения аргументов | Значения функций | |||||
| x1 | x2 | y=x1Úx2 OR | y=x1Ùx2 AND | y=x1®x2 | y=x1Åx2=x1Éx2 XOR | y=x1~x2 |
Импликация обращается в нуль, только если значение второго элемента меньше значения первого.
Функция эквивалентности равна 1 при совпадении значений обоих аргументов, а функция сложения по модулю 2 при их несовпадении.
Существуют логические функции трех, четырех и т.д. аргументов. Например,
y=x1Úx2Ú x3, y=(x1Ùx2)Ú x3, y=(x1®x2)Ù(((x2 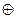 x1)Ù
x1)Ù 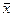 3)~
3)~ 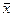 3).
3).
Первое выражение можно прочесть так: если x1 или x2 или x3 истинно (равно 1), то и y истинно (равно1).
Интерпретация второго выражения: если истинны x1 и x2 , или истинно x3, то y истинно.
Третье выражение можно прочесть так: Y истинно, если x1³x2при одновременном несовпадении x3 (отрицание x3) c логическим произведением: x1 не совпадает с x2 на не x3.
Дата добавления: 2020-08-31; просмотров: 795;











