Анализ линейной непрерывной САР
Проведем частотный анализ линейной САР, изображенной на рис. 4.7
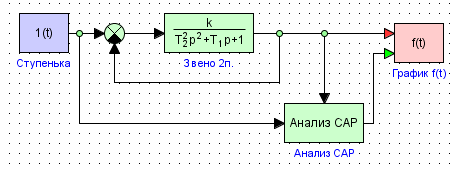
Рис. 4.8. Схема модели для анализа САР
Результаты анализа показаны на рис. 4.9
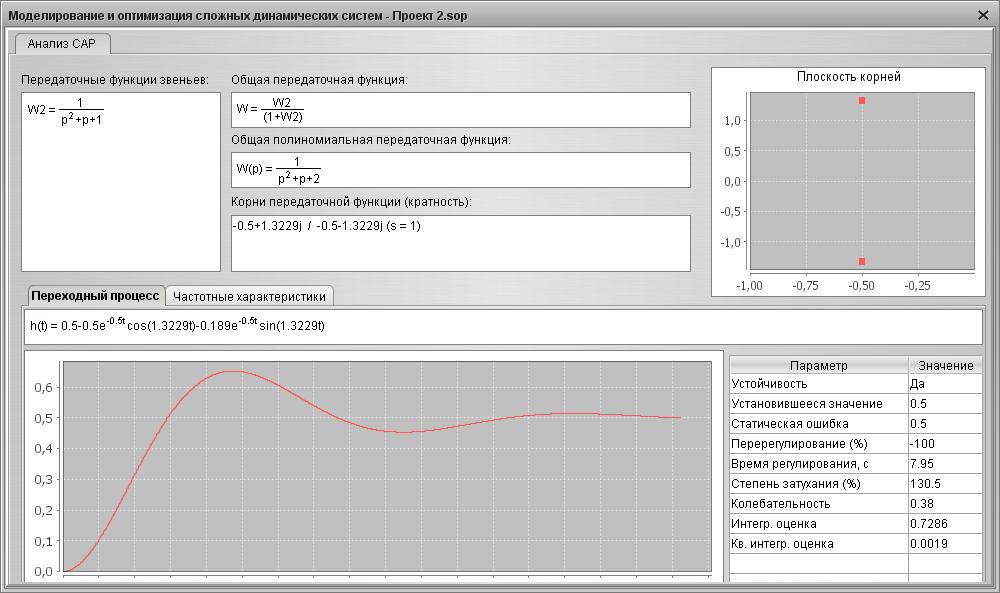
Рис. 4.9 Результаты анализа САР, переходный процесс
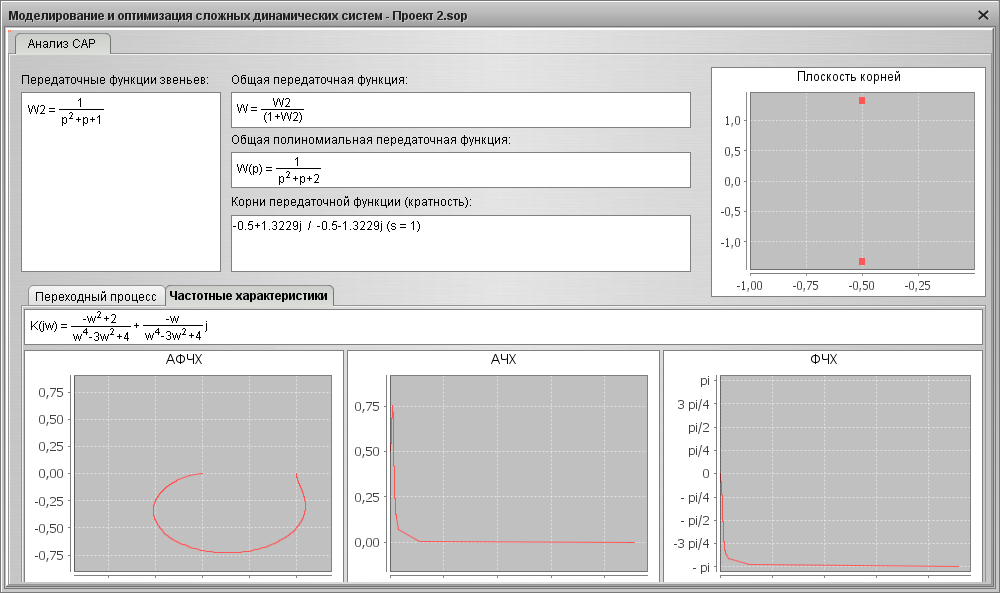
Рис. 4.10 Результаты анализа САР, частотные характеристики
На графике 4.11 показана ошибка, которую дает метод Эйлера при имитационном моделировании. Из графика следует, что наибольшая ошибка у метода возникает при наибольшей скорости изнемения производной сигнала (наибольшая вторая производная сигнала).
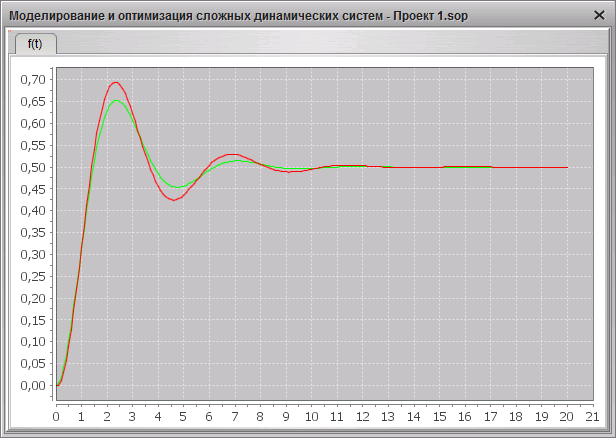
Рис. 4.11 Различия между аналитическим переходным процессом и процессом, полученным в процессе имитации
Рассчитанная суммарная ошибка составляет 0.164 (шаг = 0.1).
Изменение ошибки метода в зависимости от шага представлено в табл. 4.2
Таблица 4.2. Зависимость ошибки метода Эйлера от шага
| Шаг | Интегральная ошибка |
| 0.2 | 0.431 |
| 0.1 | 0.164 |
| 0.05 | 0.073 |
| 0.01 | 0.014 |
| 0.005 | 0.007 |
График зависимости представлен на рис. 4.12
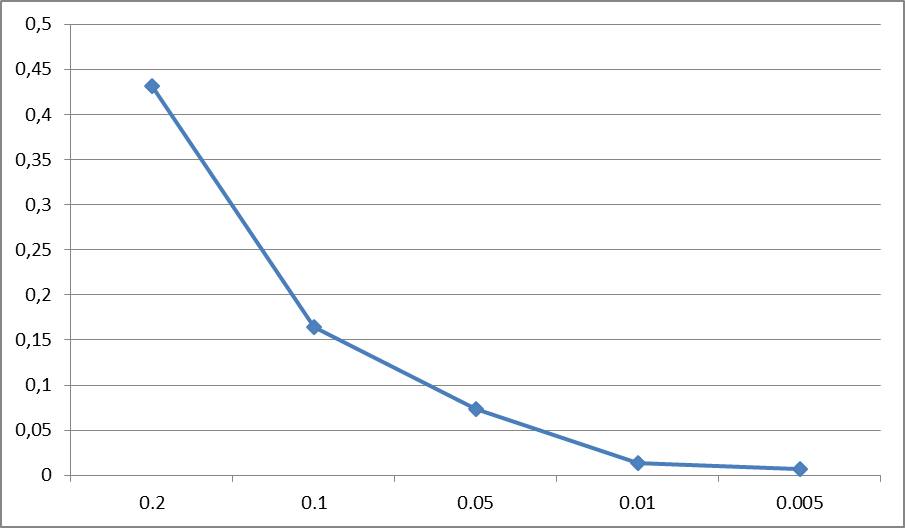
Рис. 4.12 График зависимости ошибки метода Эйлера от шага
В соответствии с проведенным анализом, очевидно, что метод Эйлера не справляется с задачей нахождения точного решения. Так как он является методом первого порядка, то уменьшение шага приводит к соразмерному уменьшению ошибки.
Для получения более точных результатов необходимо использовать методы высших порядков (метод Трапеций, метод Рунге-Кутта), однако для этого в системе моделирования необходимо реализовать итерационный решатель алгебраических уравнений.
Заключение
В данной работе была проведена разработка системы моделирования и оптимизации сложных динамических систем.
Для этого был проведен анализ существующих систем моделирования, были выявлены их достоинства и недостатки. На основании данного анализа были выдвинуты требования к разрабатываемому инструментарию. Затем были рассмотрены математические методы моделирования и оптимизации динамических систем и из них были выбраны методы, которые в дальнейшем были реализованы в системе моделирования.
На основании выдвинутых требований была разработана архитектура инструментария и определены его основные функции.
Разработанная архитектура отвечает требованию модульности, так как ее внутренняя программная структура разрабатывалась на основе интерфейсов между различными классами и более крупными частями программ. В созданной системе классов реализовано четкое разделение между графическим представлением объекта и его математической сущностью.
Архитектура также отвечает требованию открытости, разработанные модули могут успешно использоваться при разработке стороннего программного обеспечения, так как система распространяется свободно с открытым программным кодом.
Разработка приложения велась на объектно-ориентированном языке высокого уровня Java.
В системе были использованы свободно распространяемые библиотеки и компоненты, которые позволили ускорить разработку приложения.
По сравнению с другими пакетами моделирования в разработанной системе был качественно улучшен принцип организации рабочего пространства приложения, улучшен редактор моделей, позволяющий более качественно отображать элементы структурных схем.
Для проверки системы были проведены эксперименты по моделированию и оптимизации динамических систем. Было проведено сравнения аналитического метода получения переходного процесса САР и метода пошагового имитационного моделирования, рассчитаны зависимости ошибки моделирования от шага моделирования.
Разработанная система отвечает предъявленным требованиям и может быть использована в образовательном процесс на кафедре ЭВМ ТГТУ для проведения практических занятий по дисциплинам «Основы теории управления» и «Моделирование».
Дата добавления: 2021-10-28; просмотров: 655;











