Основные численные методы решения СЛАУ.

Все методы решения СЛАУ принято разделять на:

прямые (точные);
итерационные.

В прямых методах решения СЛАУ выстраивается некий последовательный алгоритм преобразования матриц (вычисления по формулам), тогда как в итерационных методах осуществляется последовательное решение СЛАУ до установления решения.

Прямые (точные) методы решения СЛАУ.

Правило Крамера.

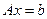
Если матрица 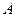- квадратная и её определитель не равен нулю, то система имеет единственное решение , координаты которого могут быть вычислены по формуле:

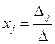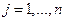, , где 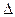- определитель матрицы 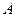, 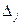- определитель матрицы, полученный из 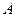заменой её 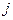-го столбца на столбец .

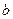Метод Крамера (метод определителей)имеет достаточно простой алгоритм, однако компьютерной реализации не получил. В методе Крамера число последовательных операций определяется формулой:

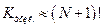, решение системы размером 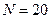может занять годы!

4.1.2 Метод обращённой (обратной) матрицы.

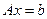
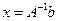
Метод обращения матрицы может быть использован для решения СЛАУ, но только для задач, где исходная матрица 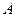не изменяется, а решение надо найти для многих правых столбцов 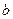. Данный метод достаточно затратный (требует много машинного времени). Поскольку при обращении матрицы реализованы алгоритмы аналогичные методу Крамера.

Метод Гаусса.

Наибольшее распространение из простых алгоритмов получил метод Гаусса. Идея метода проста и заключается в последовательном исключении неизвестных в строках матрицы. В простом методе Гаусса преобразование начинается по порядку следования уравнений.

Наиболее часто реализуется алгоритм решения СЛАУ по методу Гаусса с выборкой главных (ведущих) элементов.

Задание на лабораторную работу №2

Реализовать алгоритм метода Гаусса и решить с его помощью систему 5х5.

Сравнить полученные результаты с результатами работы подпрограммы решения СЛАУ из библиотеки IMSL.

<1 234 5 6 7 >

Дата добавления: 2020-10-25; просмотров: 261;