Итерационные методы решения СЛАУ.
Данные методы были разработаны для решения больших систем СЛАУ. Если порядок системы 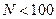 точные методы предпочтительнее по времени вычисления. Если порядок системы
точные методы предпочтительнее по времени вычисления. Если порядок системы 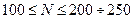 итерационные методы сопоставимы, если
итерационные методы сопоставимы, если 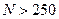 . То итерационные методы в 2 раза быстрее.
. То итерационные методы в 2 раза быстрее.
Метод простой итерации.
Рассмотрим СЛАУ с невырожденной матрицей ( 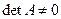 )
)
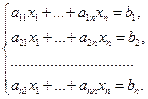
или в матричной форме: 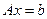
- Исходная задача
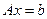 преобразуется к эквивалентному виду
преобразуется к эквивалентному виду 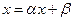 . Здесь
. Здесь 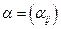 ,
, 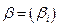 . Такое преобразование выполняется различными путями с тем условием, что
. Такое преобразование выполняется различными путями с тем условием, что 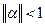 . Наиболее распространённым способом приведения системы к эквивалентному виду является следующий:
. Наиболее распространённым способом приведения системы к эквивалентному виду является следующий:
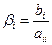 ;
; 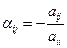 , где
, где 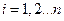 ,
, 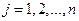 ,
, 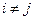
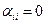 , где
, где 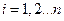
При использовании данной процедуры метод простых итераций называется методом Якоби.
В нулевом приближении за 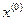 вектора неизвестных обычно принимается вектор правых частей
вектора неизвестных обычно принимается вектор правых частей 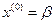 . Тогда итерационный процесс будет выглядеть как:
. Тогда итерационный процесс будет выглядеть как:
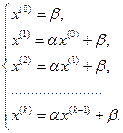
В методах итерационных процедур вводится понятие требуемой точности, она назначается программистом (пользователем):
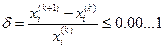
Дата добавления: 2020-10-25; просмотров: 463;











