Основные методы решения СЛАУ. Особенности численных алгоритмов.

СЛАУ – система линейных алгебраических уравнений.

Все задачи специальности (решения дифференциальных уравнений, включая уравнения в частных производных, задачи оптимизации и т.д.) всегда сводятся к СЛАУ.

Все матрицы как в левой, так и в правой части есть результат неких вычислений, т.е. в них присутствуют ошибки округления. Тогда можно говорить об устойчивости полученного решения.

Пример. Влияние погрешностей на результат решения СЛАУ.

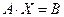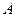Решим матричное уравнение , где - квадратная матрица коэффициентов, 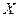и 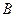- вектора.

1.

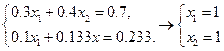
2.

3.

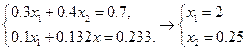
4.

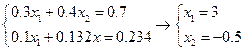
В независимости от исходной матрицы 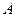полученное на ЭВМ решение всегда будет являться приближённым. Из приведённых примеров видно, что малые округления в матрицах 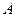и 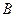могут привести к существенному изменению результата.

Для оценки устойчивости, получаемого решения вводятся понятия числа обусловленности матрицы. Для вычисления числа обусловленности матрицы в библиотеке IMSL реализована функция COND(A).

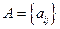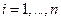Введём понятие нормы вектора. Нормой матрицы , где и 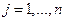называется действительное число, обозначаемое 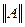и удовлетворяющая следующим условиям:

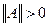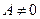1) при и 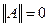тогда и только тогда, когда 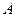- нулевая матрица;

2) 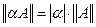для любого действительного ;

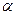3) 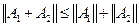, где 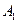, 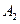- некоторые матрицы;

4)

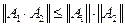
Вычисления норм матриц и векторов можно производить различными путями. Для векторов для матриц

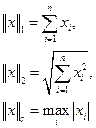
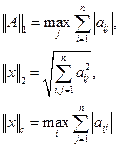
Согласование нормы матрицы с нормой векторов осуществляется с помощью неравенства: .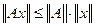

Число обусловленности матрицы определяется как: .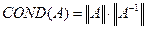

Условно можно обозначить следующие критерии обусловленности матриц:

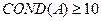- матрица хорошо обусловленная

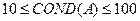- матрица плохо обусловлена. Полученные решения стоит проверить на корректность.

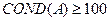- решение заведомо некорректно.

Число обусловленности характеризует степень зависимости относительной погрешности решения СЛАУ от погрешности входных данных.

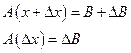
тогда

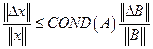
Прежде чем решать СЛАУ необходимо оценить меру обусловленности!