Эффекты расширения масштаба производства и замещения ресурсов

Как было показано, эффект расширения масштаба производства характеризует множитель 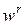; для однородной функции при r>1 эффект масштаба положителен, при r<1 - отрицателен.

Среднюю числовую характеристику эффекта масштаба можно определить аналогично коэффициентам эластичности объема выпуска по производственным факторам:

,

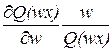а при переходе к пределу получим выражения для коэффициента эластичности производства:

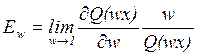. (1.3)

Эластичность производства характеризует процентный прирост продукта в некоторой точке пространства затрат ресурсов в результате их изменения на 1% (локальный эффект масштаба), так как изменение структуры ресурсов считается бесконечно малым (w®1).

Дифференцируя выражение

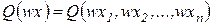
как сложную функцию переменной w, имеем:

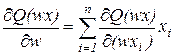. (1.4)

Подставив (1.4) в (1.3), получим:

.

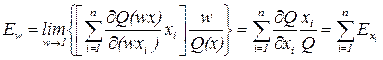Таким образом, коэффициент эластичности производства равен сумме коэффициентов эластичности объема выпуска по ресурсам производства.

С учетом выражения (1.2), это приводит к следующему выводу: коэффициент эластичности производства равен показателю эффекта расширения масштаба производства.

Особенность реальных производственных процессов состоит в возможности замещения одного фактора другим; например, существует абстрактная возможность заменить единицу производственного оборудования эквивалентным по объему фондоотдачи количеством единиц труда. Однако реальное воплощение этой абстрактной возможности зачастую неосуществимо.

Для случая двухфакторной ПФ числовая характеристика эффекта замены должна показывать, на какую величину dx₂ уменьшится объем затрат второго ресурса, если увеличить объем затрат первого ресурса на dx₁, чтобы при этом объем выпуска Q остался неизменным.

Предельной нормой замены 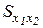(или MRTS — Marginal Rate of Substitution) одного ресурса другим называется величина

,

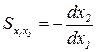показывающая, каков объем высвобождаемого ресурса при увеличении затрат ресурса-заменителя на единицу. Из условия неизменности объема выпуска при замещении факторов следует:

.

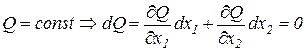Поэтому предельная норма замены равна отношению предельных продуктов факторов:

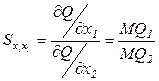. (1.5)

В данном случае х₂ является заменяемым фактором, х₁ – заменителем. Из выражения (1.5) следует, что объем высвобождаемого х₂ ресурса в расчете на единицу ресурса х₁ тем больше, чем больше предельный продукт фактора-заменителя по сравнению с предельным продуктом заменяемого фактора.

В противоположной ситуации норма замены определяется аналогично:

.

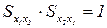Для функции Кобба-Дугласа в качестве примера получим выражение предельной замены по формуле (1.5):

.

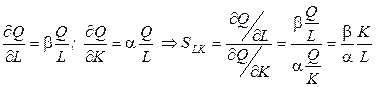Пример 1.4.1. В фирме, производящей обувь, 5 сотрудников работают на 5 станках, и выпускается 1000 пар обуви в месяц. Если коэффициенты эластичности ресурсов равны a=0,25, b=0,75, то норма замены составит (0,75*5)/(0,25*5)=3 чел./станок, то есть при приобретении дополнительно 1 станка фирма может уволить 3 рабочих, сохранив неизменный объем выпуска.

Возможность замещения ресурсов друг другом характеризует ПФ с точки зрения различных комбинаций затрат ресурсов, обеспечивающих одинаковые объемы выпуска. Количественной характеристикой темпа изменения предельной нормы замены в пространстве ресурсов является эластичность замены ресурсов:

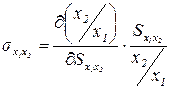. (1.6)

Эластичность замены показывает, на сколько процентов должно измениться соотношение ресурсов (при Q=const), при изменении предельной нормы замены на 1%.

Соответственно характеру изменения коэффициента эластичности замены различают два класса ПФ:

§ VES (Variable Elasticity of Substitution) – функция с переменной эластичностью замены;

§ CES (Constant Elasticity of Substitution) – функция с постоянной эластичностью замены.

Наибольшее значение имеет CES-функция, для которой возможны следующие характерные случаи: 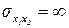, то есть пределы взаимозаменяемости ресурсов отсутствуют; 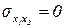, то есть ресурсы взаимодополняют друг друга и используются в строго определенном соотношении.