Экономико-математические параметры производственной функции
Производственная функция. Основные понятия
Исследование экономических процессов в современном крупномасштабном производстве требует получения большого объема статистической информации для построения математических моделей типа «затраты-выпуск», поскольку такие модели учитывают внутреннюю структуру производства. Между тем, построение матрицы внутрипроизводственных затрат во многих случаях представляет собой крайне сложную задачу. С другой стороны, зачастую гораздо проще получить отчетные данные о поведении и взаимосвязи укрупненных показателей, таких, как стоимость произведенного продукта, объем основных фондов, численность промышленно-производственного персонала и т.п. Оперируя такими укрупненными показателями и рассматривая коммерческую организацию (фирму) как «черный ящик», то есть изучая связь между объемами затраченных ресурсов и величиной произведенного продукта, можно сделать определенные выводы.
Впервые функциональная взаимосвязь между объемом производства и объемом израсходованных ресурсов была использована в производственном анализе в 1928г., в статье американских ученых экономиста Пола Дугласа и математика Чарльза Кобба «Теория производства». В этой статье была предпринята попытка определить эмпирическим путем влияние величин затраченного капитала и труда на объем выпускаемой продукции в обрабатывающей промышленности США. Были использованы статистические данные за 1899-1922 г.г. и поставлены следующие задачи:
1.Определить вид функций, наиболее точно выражающих количественные соотношения между тремя выбранными характеристиками производства.
2.Найти значения коэффициентов конкретной функции этого вида.
3.Проверить достоверность значений функции, сравнив их с фактическими данными.
Ч. Коббом была предложена функция вида:
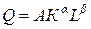 ,
,
где Q – объем выпускаемой продукции; К – объем основного капитала; L – затраты труда; А, a, b - коэффициенты, удовлетворяющие условиям:
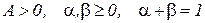 .
.
коэффициент А, предназначен для перевода единиц измерения труда и капитала в единицы измерения продукта; коэффициенты a, b отражают вклад труда и капитала в изготовление продукта.
С использованием метода наименьших квадратов были определены значения числовых коэффициентов:
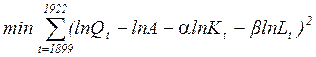 .
.
При этом оказалось, что А=1,01, a=0,25, b=0,75, то есть функция имеет вид
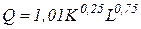 .
.
Сравнение величины Q(K,L) с фактическим значением объема производства показало удовлетворительную достоверность расчетов на основе производственной функции.
| Определение производственной функции |
Производственной функцией (ПФ) производственного процесса в общем виде называется отображение
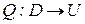 ,
,
моделирующее выпуск продукции в данном процессе. Область определения функции D представляет собой множество производственных ресурсов 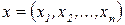 в стоимостном или натуральном выражении. Область значений функции U включает в себя область количественных оценок результатов производства, например, физический объем выпуска по каждому наименованию ассортимента или стоимостные показатели
в стоимостном или натуральном выражении. Область значений функции U включает в себя область количественных оценок результатов производства, например, физический объем выпуска по каждому наименованию ассортимента или стоимостные показатели 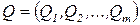 .
.
Несмотря на широту введенного определения ПФ, наиболее исследованы функции для случая m=1, то есть имеется единственная (агрегированная) количественная оценка результатов производства. В этом ПФ представляет собой обычную функцию нескольких переменных.
Определение ПФ: зависимость между объемом выпуска продукции Q и количествами затраченных производственных ресурсов 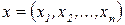 :
:
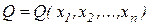 .
.
Следует учесть, что значение объема выпущенной продукции предполагается максимально возможным при данных затратах производственных ресурсов, то есть непроизводительные («холостые») затраты отсутствуют. Графически поверхность выпуска, формируемая ПФ, изображена на рис. 1.1.
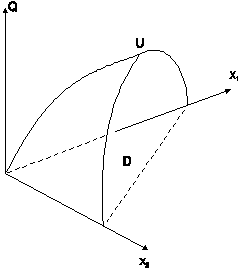 |
Рис. 1.1. Графическая интерпретация ПФ
Зависимость, моделирующая реальный производственный процесс, имеет следующие свойства:
1. При увеличении объема затрат одного из ресурсов и неизменном объеме затрат других ресурсов выпуск продукции возрастает:
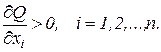
Это свойство вытекает из гипотезы рационального выбора производителем ресурсов производства – ресурсы, не увеличивающие выпуск продукции, не применяются в процессе производства.
Пример 1.1.1. Фирма, занимающаяся производством мебели, использует в качестве ресурсов труд рабочих и оборудование. В случае приобретения дополнительно деревообрабатывающего станка объем продукции фирмы должен возрасти, если только этот станок не выпускает бракованную продукцию.
2. При фиксированных объемах затрат всех ресурсов кроме одного последовательное увеличение этого ресурса обеспечивает постоянно снижающееся приращение величины продукта
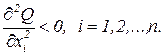
Данное свойство обусловлено необходимостью сбалансированности затрат ресурсов в конкретном технологическом процессе: увеличение затрат одного ресурса без соответствующего роста затрат другого ресурса не обеспечивает технологию фирмы полноценным потоком ресурсов; следовательно дополнительный эффект от увеличения затрат ресурса снижается.
Пример 1.1.2. В фирме, производящей обувь, работает 5 рабочих и используется 5 станков. В случае приобретения дополнительно одного станка объем продукции фирмы должен возрасти на 100 пар обуви в месяц. Если же вначале на 5 рабочих приходилось 20 станков, то приобретение дополнительно одного станка повысит объем производства только на 40 пар обуви в месяц, поскольку количество рабочих, обслуживающих станки, не изменилось.
Геометрическая интерпретация этих условий приведена на рис. 1.2, на котором изображена зависимость величины произведенного продукта от объема затрат одного ресурса при фиксированных значениях затрат других ресурсов; эта зависимость называется кривой выпуска. Первое условие означает, что касательная к кривой выпуска при всех возможных значениях расхода ресурса имеет положительный наклон, поскольку 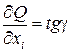 .
.
Второе условие, преобразованное к виду
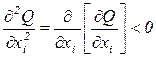 ,
,
показывает, что прирост продукта в расчете на дополнительные затраты единицы ресурса снижается при росте затрат ресурса.
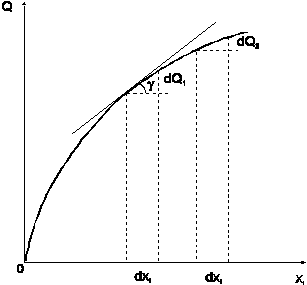
Рис. 1.2. Кривая выпуска
Экономико-математические параметры производственной функции
Основные характеристики ПФ рассматриваются на примере функции:
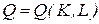 .
.
| Средние величины |
Средние продукты характеризуют удельный эффект использования ресурсов в производственном процессе фирмы.
Средняя производительность труда – это отношение произведенного продукта к количеству затраченного труда:
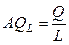 .
.
Средняя фондоотдача – это отношение объема произведенного продукта к стоимости основных фондов:
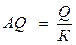 .
.
Для функции Кобба-Дугласа средняя производительность труда равна:
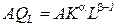
и в силу условия b<1 является убывающей функцией аргумента L. Другими словами, с увеличением трудозатрат средняя производительность труда падает, поскольку величина второго ресурса К остается неизменной, и привлекаемая рабочая сила не обеспечивается дополнительными средствами производства; фондовооруженость 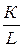 при этом снижается. Аналогично интерпретируется средняя фондоотдача.
при этом снижается. Аналогично интерпретируется средняя фондоотдача.
Пример 1.2.1. В фирме, производящей обувь, 5 рабочих работает на 5 станках, и выпускается 1000 пар обуви в месяц. Поэтому средняя производительность труда одного рабочего составит (1000/5)=200 пар/чел. Фондовооруженость при этом равна (5/5)=1 станок/чел. Предположим, что нанято ещё 5 рабочих, в результате чего выпуск продукции увеличился до 1500 пар обуви в месяц. Средняя производительность труда рабочего снизится до (1500/10)=150 пар/чел. Фондовооруженость уменьшится (5/10)=0,5 станок/чел.
Геометрически среднее значение спродукта интерпретируется как угловой коэффициент секущей линии, проведенной из начала координат к точке кривой выпуска, характеризующей определенное значение продукта 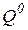 , то есть из рис. 1.3 следует, что:
, то есть из рис. 1.3 следует, что:
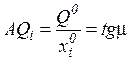 .
.
| Предельные величины |
Предельные продукты характеризуют эффект в виде прироста объема продукции, получаемый от увеличения затрат ресурсов.
Предельная производительность труда – характеризует величину дополнительного эффекта от каждой затраченной единицы труда при данном сочетании ресурсов (К,L):
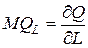 .
.
Исходя из определения ПФ при увеличении затрат труда предельная производительность труда снижается. Геометрически предельный продукт, как показано на рис. 3, представляет собой угловой коэффициент касательной к кривой выпуска в данной точке
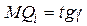 .
.
Для функции Кобба-Дугласа предельная производительность равна:
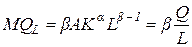 ,
,
то есть предельная производительность пропорциональна средней и всегда меньше ее, так как b<1 (рис. 1.4).
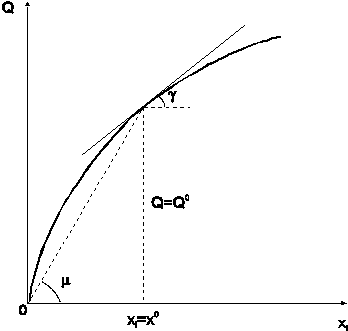
Рис. 1.3. Геометрический смысл средних и предельных величин
Предельная фондоотдача определяется аналогично:
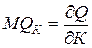 .
.
Пример 1.2.2. Фирма, рассмотренная в примере 1.2.1, нанимает дополнительного рабочего. Если коэффициент b=0,75, то увеличение продукции (предельная производительность) составит (0,75*200)=150 пар/чел. Если же фирма, имея 10 рабочих, наймет дополнительного рабочего, то увеличение продукции составит (0,75*150)=113 пар/чел.
| Коэффициенты эластичности |
Большое значение для анализа ПФ имеют безразмерные коэффициенты, характеризующие процент прироста объема выпуска продукции при увеличении затрат ресурса на 1%, то есть коэффициенты эластичности.
Эластичность продукта по фондам определяется по формуле:
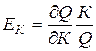 .
.
Поскольку при неизменном объеме трудозатрат относительному увеличению объема основных фондов на 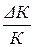 соответствует относительное увеличение выпуска на
соответствует относительное увеличение выпуска на 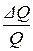 , то относительное приращение выпуска составит
, то относительное приращение выпуска составит 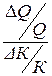 , а переходя к пределу при DK®0, получим выражение эластичности.
, а переходя к пределу при DK®0, получим выражение эластичности.
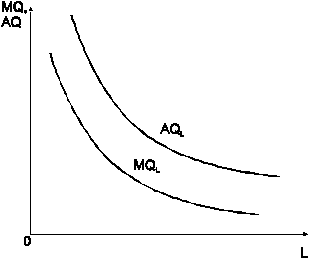 |
Рис. 1.4. Средний и предельный продукты функции Кобба-Дугласа
Эластичность продукта по труду
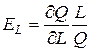
имеет аналогичное значение.
Параметры функции Кобба-Дугласа являются коэффициентами эластичности:
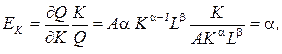
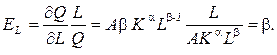
Поэтому для функции Кобба-Дугласа коэффициенты a, b постоянны и не зависят от объема факторов К, L.
Пример 1.2.3. Фирма, рассмотренная в примере 1.2.1, планирует увеличить штат персонала на 10%. Если эластичность продукта по труду b=0,75, то увеличение продукции в результате составит (0,75*10)=7,5%. Можно сформулировать обратную задачу: на сколько процентов следует увеличить штат фирмы, если прирост объема производства должен составить 7,5%? Очевидно, количество работников должно возрасти на (7,5/0,75)=10%.
Дата добавления: 2020-10-25; просмотров: 470;











