Дополнительные свойства производственной функции

Помимо условий, включенных в определение ПФ, на вид функции, как правило, накладываются дополнительные ограничения.

Свойство однородности состоит в том, что при увеличении затрат всех ресурсов в одинаковое количество раз w объем продукции возрастает в кратное w количество раз:

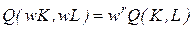
для любого w>1. Показатель r>0 называют степенью однородности функции Q и характеризует эффект расширения масштаба производства: если r>1, то увеличение всех ресурсов в w раз приводит к возрастанию объема выпуска более чем в w раз, то есть эффект масштаба положителен; если r<1, то прирост факторов в w раз обеспечивает менее чем w-кратное возрастание объема выпуска, то есть эффект масштаба отрицателен.

Пример 1.3.1. Фирма, выплавляющая металл, использует в качестве ресурсов труд рабочих и оборудование. В случае увеличения штата фирмы и парка оборудования в 2 раза объем продукции фирмы возрос в 4 раза. Следовательно, фирма характеризуется положительным эффектом масштаба с коэффициентом r=2 (так как 2²=4).

Наиболее употребительными являются линейно-однородные ПФ, для которых

,

то есть эффекта расширения масштаба производства не наблюдается.

Свойство необходимости всех ресурсов:

,

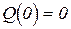то есть при отсутствии хотя бы одного из ресурсов выпуск продукции отсутствует.

Пример 1.3.2. Фирма, выплавляющая металл, согласно технологии использует в качестве сырья железную руду и топливо. Поскольку оба ресурса необходимы для производства, то производство будет остановлено в случае непоставки хотя бы одного из них.

Свойство ограниченного роста (вогнутость): при возрастании ресурса от нуля до конечного значения происходит стремительный рост объема выпуска, который затем сходит на нет

.

Условие вогнутости (так называемое условие ненасыщаемости) выражает неэффективность резервирования ресурсов.

Пример 1.3.3. На целлюлозобумажном комбинате объем производства бумаги зависит от затрат используемой целлюлозы (х₁) и количества станков (х₂) по функции Q=х₁^aх₂^b, a=0,5, b=0,1. При плановом режиме загрузки в месяц потребность в ресурсах составляет 20 тонн целлюлозы и 10 станков. Поэтому выпуск продукции достигает 20^0,510^0,1=5,6 тонн. Предельный продукт второго ресурса MQ₂=¶Q/¶x₂=bх₁^aх₂^b-1=0,1*20^0,5*10^-0,9=0,06т/станок, то есть прирост продукции от приобретения дополнительного станка составит 0,06 тонн. Если фирма приобретет 100 станков, не обеспечив это расширение станочного парка увеличением поставок целлюлозы, то эффект от последнего приобретенного станка составит MQ₂=0,1*20^0,5*(10+99)^-0,9= 0,007т/станок. Поэтому резервирование ресурса окажется неэффективно.

Линейно-однородные ПФ в соответствии с теоремой Эйлера могут быть представлены в виде:

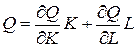. (1.1)

Экономически это можно интерпретировать следующим образом: пусть общество состоит из рабочих и капиталистов; капиталист вкладывает капитал в производство до тех пор, пока дополнительный доход 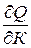не достигнет установившейся в экономике нормы прибыли, то есть произведение нормы прибыли 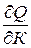на вложенный капитал К представляет собой доход капиталистов. Аналогично, нанимая рабочих, капиталист увеличивает их численность до тех пор, пока дополнительный доход 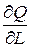, приносимый очередным рабочим, не достигнет его заработной платы, то есть теория предельной производительности труда утверждает, что 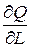есть заработная плата, поэтому слагаемое 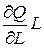представляет собой доход рабочих, общая численность которых L. В таком случае Q – суммарный доход членов общества.

Для теории производства уравнение (1.1) означает, что объем продукции складывается из частей, произведенных за счет использования каждого ресурса в отдельности.

Разделив обе части (*) на Q, имеем:

, (1.2)

то есть для линейно-однородной функции коэффициенты эластичности

,

если хотя бы один из них больше нуля.

Для однородной функции 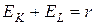, то есть сумма показателей эластичности определяется степенью однородности функции, то есть типом эффекта расширения масштаба производства.

Таким образом, получено важное свойство коэффициентов эластичности ресурсов функции Кобба-Дугласа: сумма коэффициентов эластичности равна показателю эффекта расширения масштаба:

.

Пример 1.3.4. Объем продукции фирмы, рассмотренной в примере 1.3.3, при увеличении обоих ресурсов на 1% возрастет на r=a+b=0,5+0,1=0,6%.