Виды производственных функций
Рассмотрим основные виды ПФ, нашедших применение в практике экономического анализа производственных процессов, на примере функций двух ресурсов, поскольку они допускают наглядную геометрическую интерпретацию.
1. Линейная функция
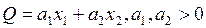 .
.
Коэффициенты линейной функции представляют собой значения предельных продуктов, так как
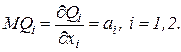
Это означает, что прирост объема выпуска в результате единичного увеличения объема затраченного ресурса постоянен и не зависит от исходного объема факторов. Предельная норма замены для линейной ПФ постоянна и равна 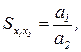 а эластичность замещения факторов бесконечна
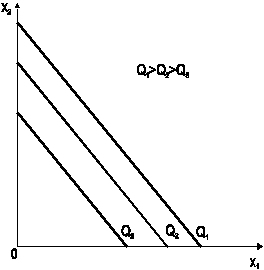
а эластичность замещения факторов бесконечна 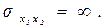 Изокванты линейной функции изображены на рис. 1.8а.
Изокванты линейной функции изображены на рис. 1.8а.
Линейная ПФ применяется обычно при моделировании крупномасштабных систем (крупная отрасль, экономика в целом), в которых выпуск продукции является результатом одновременного использования множества различных технологий. Особое значение имеет предположение о постоянстве предельных производительностей ресурсов и их неограниченной замещаемости.
Пример 1.6.1. Предприятие за последние 3 года показало следующие хозяйственные результаты:
| Год | Объем металла, тыс. тонн | Количество станков, единиц | Персонал, тыс. чел. |
| 0,8 | |||
| 1,8 | |||
| 2,8 |
Определить значения коэффициентов ПФ, объяснить их экономический смысл. Спрогнозировать объем металла в 4-й год, если запланировано довести количество прессов до 40 ед., численность работников до 3,5 тыс. чел.
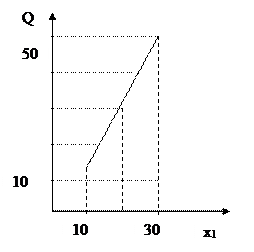
Построив графики зависимости объема выпуска от затрат ресурсов, приходим к выводу, что для данного предприятия характерна линейная функция от ресурсов  (оборудование) и
(оборудование) и 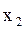 (персонал):
(персонал): 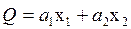 .
.
 Составим функцию суммы квадратов отклонений:
Составим функцию суммы квадратов отклонений: 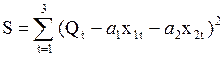 . Найдем производные этой суммы по неизвестным коэффициентам
. Найдем производные этой суммы по неизвестным коэффициентам 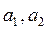 и приравняем их к нулю:
и приравняем их к нулю:
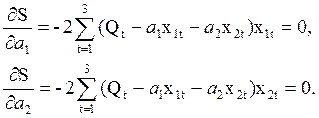
Рис. 1.7. Пояснение к примеру 1.6.1
После преобразования получим:
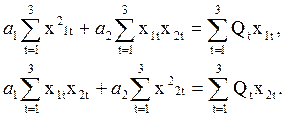
Найдем из условий задачи суммы в этих уравнениях и подставим в систему:
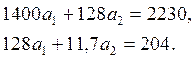
Решение этой системы уравнений позволяет получить 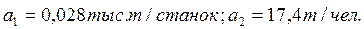 Объем металла в 4-й год равен:
Объем металла в 4-й год равен:
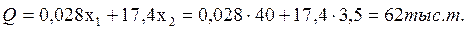 .
.
2. Функция Кобба-Дугласа
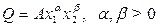 .
.
Коэффициент А представляет собой параметр шкалы (А>0); коэффициенты a,b суть коэффициенты эластичности выпуска по ресурсам. Предельный продукт факторов пропорционален их среднему продукту:
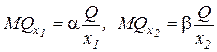 .
.
Предельная норма замены равна (для линейно-однородной функции)
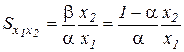 ,
,
поэтому эластичность замещения составляет
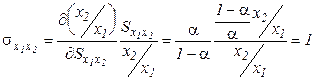 ,
,
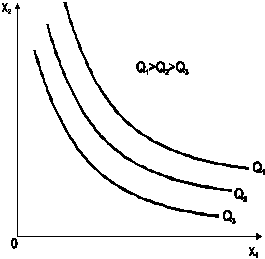
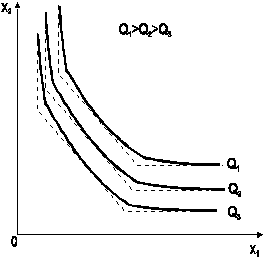
то есть замещение данного фактора другим происходит в пропорции 1:1. В этом заключается недостаток такого рода ПФ: они не всегда верно отражают реальные экономические процессы, так как не всегда один фактор можно заменить эквивалентным количеством другого. Изокванты функции Кобба-Дугласа изображены на рис. 1.8б.
Функция Кобба-Дугласа чаще всего используется для описания среднемасштабных хозяйственных субъектов (корпорация, отрасль), характеризующихся устойчивым, стабильным функционированием, когда вовлечение дополнительной единицы ресурса приносит эффект, пропорциональный средней производительности имеющегося ресурса.
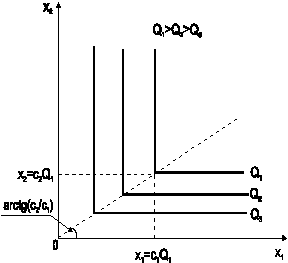
3. Функция с фиксированными пропорциями (функция Леонтьева):
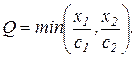
Коэффициенты сi выражают количество i-го ресурса, необходимого для производства единицы продукта. Функция Леонтьева выражает решение задачи линейного программирования, возникающей в модели “затраты–выпуск”:
сiQ £ xi, Q ® max,
Рис. 1.9. Пояснение к примеру 1.6.2
поскольку фактор, ограничивающий объем выпуска, определяется условием минимальности. Эластичность замены факторов по любому ресурсу s = 0, как видно из геометрической интерпретации функции Леонтьева на рис. 1.8в.
Предельный продукт является кусочно-постоянной двухуровневой функцией соотношения 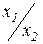 (фондовооруженности):
(фондовооруженности):
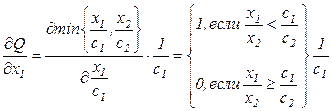 .
.
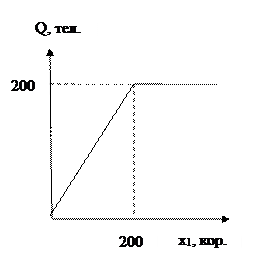
Пример 1.6.2. На конвейере сборка телевизоров осуществляется путем соединения корпуса и кинескопа, то есть имеется фиксированная пропорция использования ресурсов с1=с2=1 (1:1). Если на сборку поступило 200 корпусов и 500 кинескопов в месяц, то, по функции Леонтьева, будет собрано 200 телевизоров. Предельный продукт первого ресурса (корпусов) в этом случае равен 1, то есть дополнительно полученный со склада корпус позволит собрать 1 телевизор; предельный продукт второго ресурса (кинескопов) равен нулю, так как кинескопы имеются в избытке. Кривая выпуска показана на рис. 1.9.
(а) (б)
(в) (г)
Рис. 1.8. Изокванты производственных функций
Функция Леонтьева предназначена для моделирования строго детерминированных технологий, не допускающих отклонения от технологических норм использования ресурсов на единицу продукции; обычно используются для описания мелкомасштабных или полностью автоматизированных производственных объектов.
Дата добавления: 2020-10-25; просмотров: 586;











