Изолинии производственных функций
Изолинии представляют собой кривые, во всех точках которых соответствующая функция имеет постоянное значение того или иного параметра.
| Линия постоянного продукта |
Изокванта – это множество точек плоскости ресурсов, удовлетворяющих условию постоянства объема выпуска:
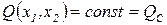 .
.
Уравнение изокванты в явном виде записывается как
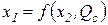 .
.
Вид изокванты показан на рис. 1.5. Например, для функции Кобба-Дугласа уравнение изокванты в явном виде выглядит следующим образом:
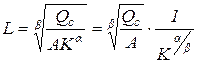 .
.
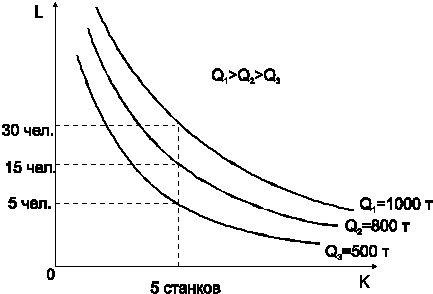 |
Рис. 1.5. Изокванта
Экономический смысл изокванты заключается в том, что кривая показывает объем трудовых ресурсов, необходимых для получения продукта Qс в зависимости от располагаемого объема капитала К.
Пример 1.5.1. Для фирмы, выплавляющей металл, построены изокванты при выплавке 500, 800 и 1000 тонн металла в месяц (рис. 1.5). По рис. можно определить, что при наличии 5 станков для выплавки 500 т в месяц требуется 5 рабочих, а для выплавки 1000 т – 30 рабочих.
Свойства изокванты:
1. Если все ресурсы необходимы для производства продукта, то нет такого объема выпуска Qс, для которого изокванта имеет общие точки с осями координат. Это свойство вытекает из условия необходимости всех ресурсов.
2. Большему значению объема выпуска Qс соответствует более удаленная от начала координат изокванта, что следует из условия однородности.
3. Изокванты, соответствующие различным значениям Qс, не пересекаются.
| Линия постоянного наклона изокванты |
Изоклина – это множество точек плоскости ресурсов, в которых наклон изоквант при различных значениях объема выпуска остается постоянным; поскольку наклон графика функции выражает производная, то изоклина – множество точек, в которых
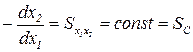 .
.
Таким образом, геометрический смысл предельной нормы замены, как показано на рис. 1.6, состоит в том, что 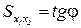 .
.
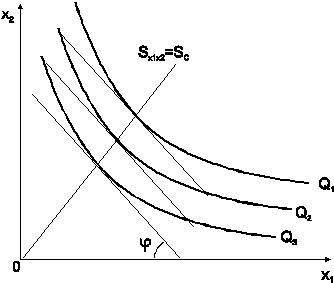 |
Рис. 1.6. Изоклина
Например, для функции Кобба-Дугласа, как было показано выше, предельная норма замены пропорциональна значению коэффициента фондовооруженности 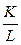
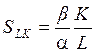 ,
,
то есть чем большей величиной основного капитала (фондов) в расчете на одного работника располагает предприятие, тем большая часть капитала может быть высвобождена и инвестирована в другие проекты при увеличении персонала на одного работника.
Следовательно, уравнение изоклины функции Кобба-Дугласа определяется следующим угловым коэффициентом:
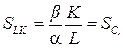 .
.
Дата добавления: 2020-10-25; просмотров: 540;











