Функция издержек в долгосрочном периоде
| Задача определения функции издержек |
Функция издержек определяется в результате решения задачи минимизации издержек на производство фиксированного выпуска Q. Эту задачу можно записать в виде
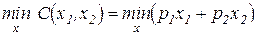
при условии, что 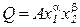 ,
, 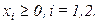
| Геометрическая интерпретация |
Эта задача имеет наглядную геометрическую интерпретацию (рис. 2.3). Если перемещать изокосту по направлению к началу координат до тех пор, пока она продолжает иметь общие точки с изоквантой, соответствующей фиксированному объёму выпуска Q1, то решением задачи минимизации издержек будет общая точка A1 изокосты C1 и изокванты Q1 с координатами [x1*(Q1), x2*(Q1)]. Эта точка касания зависит от объёма выпуска (поэтому записано [x1*(Q1), x2*(Q1)] ). Если объём выпуска уменьшится до уровня Q2 (Q2<Q1), то изменится положение точки касания на A2 с координатами [x1*(Q2), x2*(Q2)]. Множество точек Ai, i=1,2,...,n, соответствующих различным объемам выпуска Qi, i=1,2,...,n, образуют линию долгосрочного развития фирмы.Точки, находящиеся на этой линии, характеризуют минимальные издержки производства, соответствующие фиксированным объемам выпускаемойпродукции.
Изокванты на этом графике характеризуют технологические ограничения, т.е. каждая i-я изокванта отображает все комбинации ресурсов х1 и х2, с помощью которых можно обеспечить выпуск Qi. Изокосты характеризуют экономическиеограничения, т.е. каждая i-я изокоста отображает все комбинации ресурсов х1 и х2,имеющие при неизменных ценах ресурсов один и тот же уровень издержек Ci. Поскольку задача минимизации издержек сводится к нахождению точки, в которой изокванта касается самой низкой изокосты, то это будет означать, что комбинация ресурсов, соответствующая точке касания, обеспечит потребный выпуск при минимальных издержках. Тогда комбинация ресурсов [x1*(Q1), x2*(Q1)], соответствующая точке А1, обеспечит минимальные издержки на уровне С1 выпуску Q1, а комбинация ресурсов [x1*(Q2), x2*(Q2)], соответствующая точке А2, – на уровне С2 выпуску Q2.

Рис. 2.3. Траектория долговременного развития
Сформулируем условие касания: наклон изокванты должен быть равен наклону изокосты.Поскольку угол наклона изокванты определяется выражением 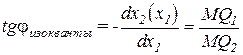 , а угол наклона изокосты, исходя из уравнения этой кривой,
, а угол наклона изокосты, исходя из уравнения этой кривой,
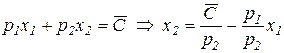
равен 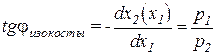 , то при
, то при 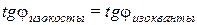 выполняется условие:
выполняется условие:
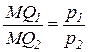 . (2.2)
. (2.2)
Таким образом, долгосрочная траектория развития организации образована точками сочетаний ресурсов, отношение предельных продуктов которых при данном виде производственной функции равно отношению цен этих ресурсов.
| Функции спроса на ресурсы |
Выразим известный фиксированный выпуск Q в точке рыночного равновесия через оптимальные объёмы используемых ресурсов
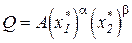 . (2.3)
. (2.3)
Подставим выражения предельных продуктов MQ1, MQ2 (см. пример 1.3.3.) в условие минимальности издержек (2.2), и выразим x2*:
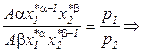
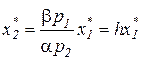 , (2.4)
, (2.4)
где 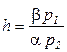 .
.
Уравнение
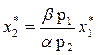
выражает линию долгосрочного развития.
Подставим x2* из (2.4) в ПФ (2.3), откуда найдем x1* как функцию объема выпуска: 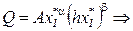
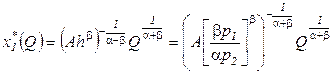 . (2.5)
. (2.5)
Выражение x2*(Q*) определим, используя соотношение x2*=hx1*:
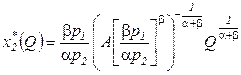 . (2.6)
. (2.6)
Найденные значения 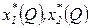 представляют собой функции спроса на ресурсы. Они позволяют для известного значения объема выпуска Q определить необходимые количества ресурсов, при которых достигается минимум издержек.
представляют собой функции спроса на ресурсы. Они позволяют для известного значения объема выпуска Q определить необходимые количества ресурсов, при которых достигается минимум издержек.
| Функция издержек |
Подставим значения 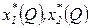 в выражение функции издержек
в выражение функции издержек
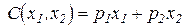 ,
,
получим зависимость суммы затрат организации от объема выпуска продукции:
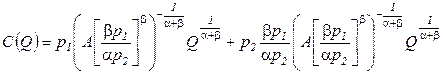 ,
,
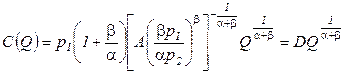 , (2.7)
, (2.7)
где 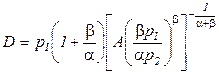 . Выражение (2.7) представляет собой функцию издержек. Необходимо подчеркнуть, что она является функцией выпуска C(Q), а не функцией затрачиваемых ресурсов C(x1,x2). Полученная функция издержек соответствует длительному периоду, то есть
. Выражение (2.7) представляет собой функцию издержек. Необходимо подчеркнуть, что она является функцией выпуска C(Q), а не функцией затрачиваемых ресурсов C(x1,x2). Полученная функция издержек соответствует длительному периоду, то есть 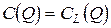 .
.
В случае отсутствия эффекта расширения масштаба r=a+b=1 функция издержек представляет собой линейную функцию объема выпуска Q:
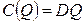 .
.
Кривая функции издержек выпукла вверх при r>1; это означает, что при увеличении объема выпуска продукции происходит относительное уменьшение издержек, то есть наблюдается положительный эффект расширения масштаба производства. В случае r<1 кривая функции издержек выпукла вниз, что соответствует относительно более быстрому темпу роста издержек по сравнению с ростом объема производства.
Пример 2.2.1. Для стекольного завода, приобретающего песок по цене 4 тыс. руб./т и топливо по цене 7 тыс. руб./т, определить характер кривых долгосрочных издержек CL(Q) при различных типах эффекта расширения масштаба: отсутствие эффекта расширения масштаба (r=1) 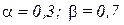 ; возрастающая отдача от расширения масштаба (r=1,2)
; возрастающая отдача от расширения масштаба (r=1,2) 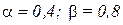 ; убывающая отдача от расширения масштаба (r=0,8)
; убывающая отдача от расширения масштаба (r=0,8) 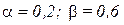 .
.
Зависимости долгосрочных издержек от объема выпуска продукции (в тоннах) изображена на рис. 2.4. Функции издержек построены с использованием формула (2.7), полагая А=1. Очевидно, что при возрастающей отдаче от расширения производства издержки фирмы растут замедленными темпами по сравнению с ростом объема выпуска, а в случае убывающей отдачи – ускоренными темпами. Графики на рис. 2.4 позволяют определить суммы издержек при различных объемах производства: например, при выпуске 4 тонн стекла в месяц фирма, работающая в экономичном режиме, затратит 45 тыс. руб. (если эффект расширения масштаба отсутствует).
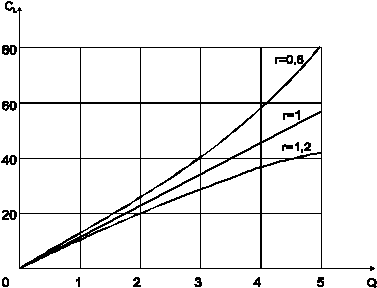
Рис. 2.4. Кривые долгосрочных издержек
Дата добавления: 2020-10-25; просмотров: 514;











