Метод интегрирования заменой переменной.
Заметим, что для интегрирования некоторых функций нужно пользоваться заменой переменной. Ниже подобный метод интегрирования покажем на примерах.
Пример 5.25.Вычислить неопределенный интеграл 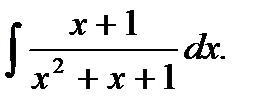
Решение.

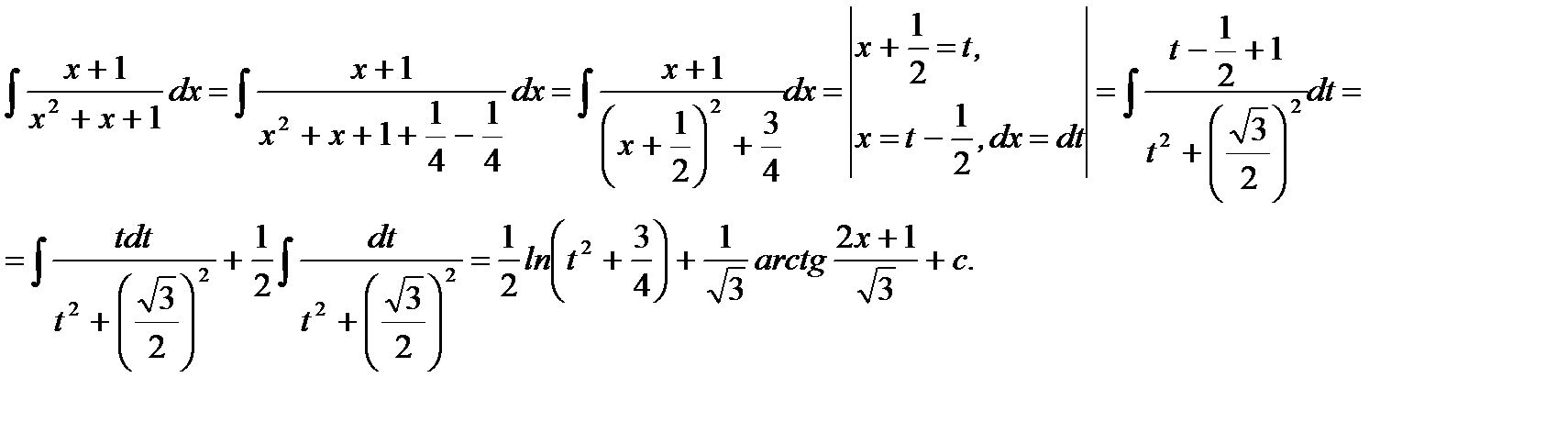
Ответ: 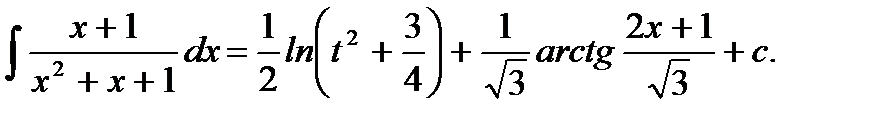
Пример 5.26.Вычислить неопределенный интеграл 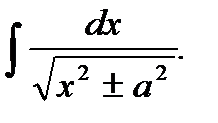
Решение.
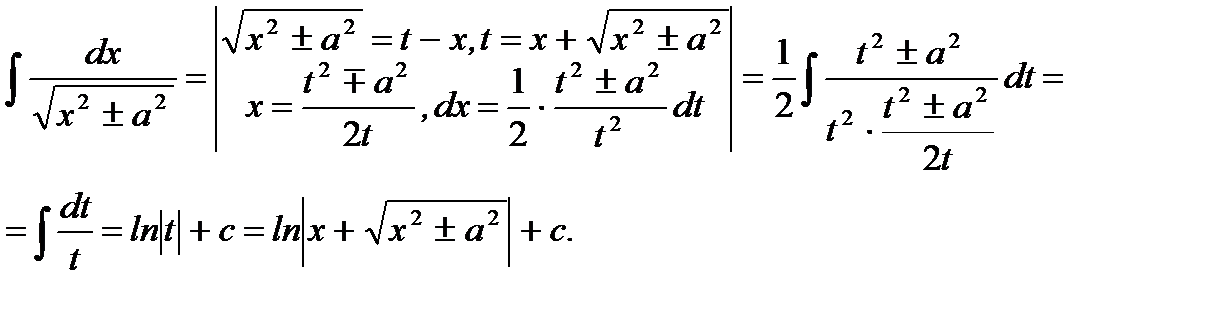 (5.33)
(5.33)
Ответ: 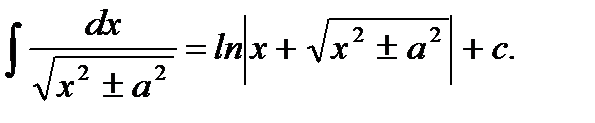
Пример 5.27.Вычислить неопределенный интеграл 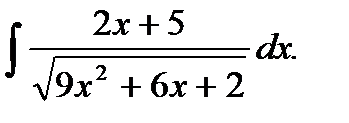
Решение.
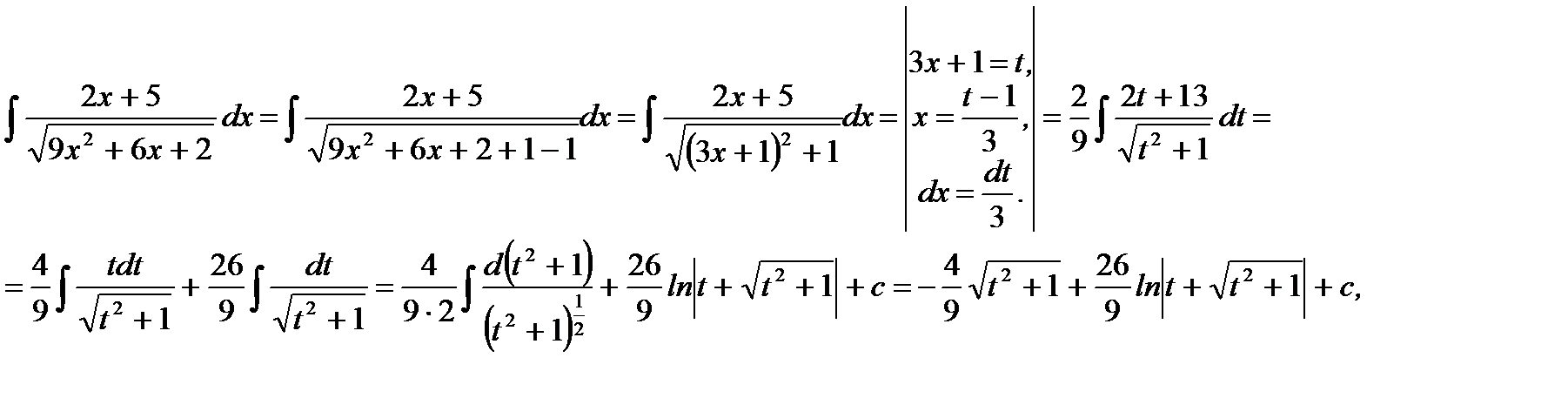
где 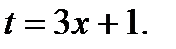 Отметим, что
Отметим, что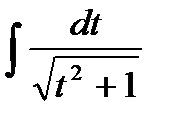 вычислен согласно формуле (5.33).
вычислен согласно формуле (5.33).
Ответ: 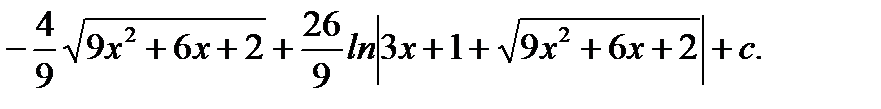
Пример 5.28.Вычислить неопределенный интеграл 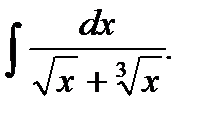
Решение.
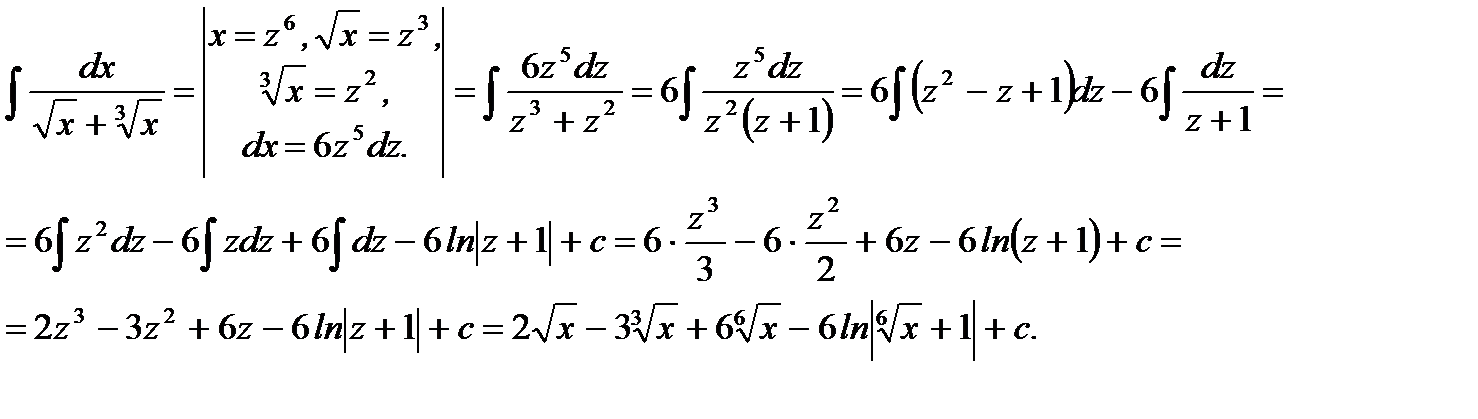
Ответ: 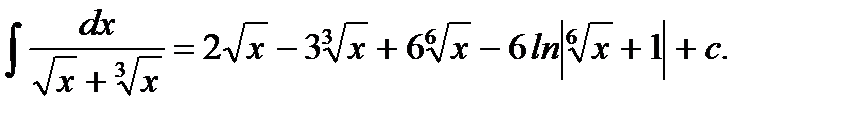
Пример 5.29.Вычислить неопределенный интеграл 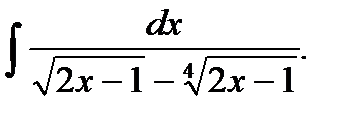
Решение.
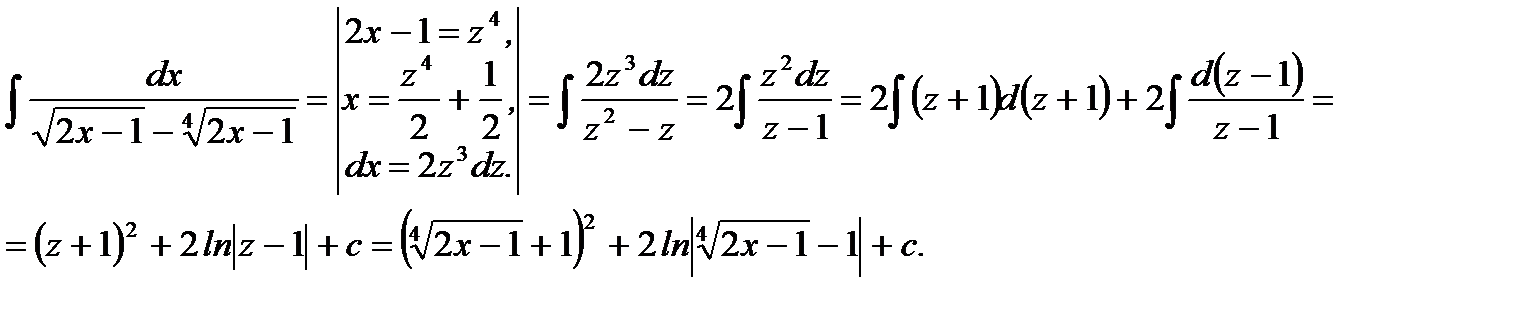
Ответ: 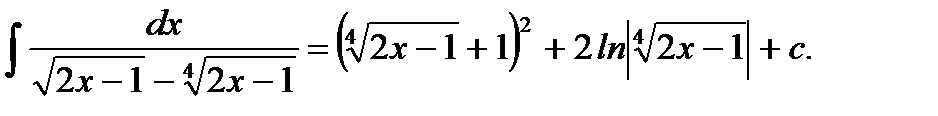
Интегрирование тригонометрических функций.
Для вычисления интеграла 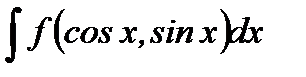 , где подынтегральная функция является рациональной функцией от
, где подынтегральная функция является рациональной функцией от 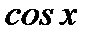 и
и 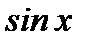 , нужно пользоваться следующими подстановками:
, нужно пользоваться следующими подстановками:
1. 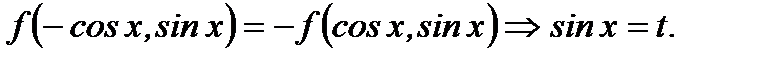
2. 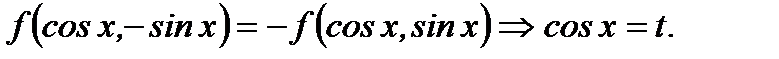
3. 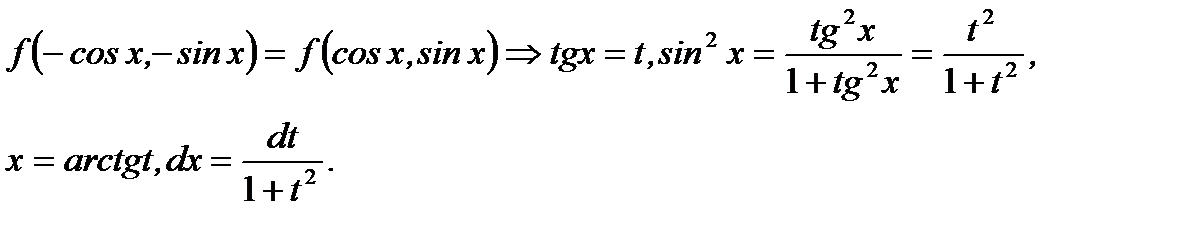 (5.34)
(5.34)
4. 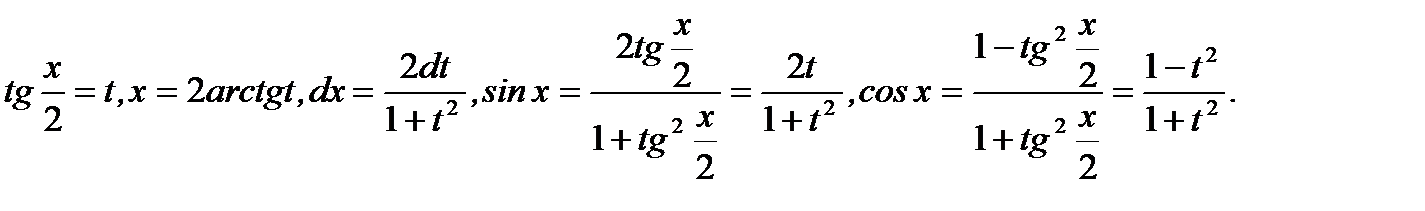
Пример 5.30.Вычислить неопределенный интеграл 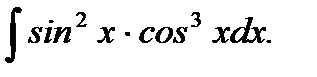
Решение.
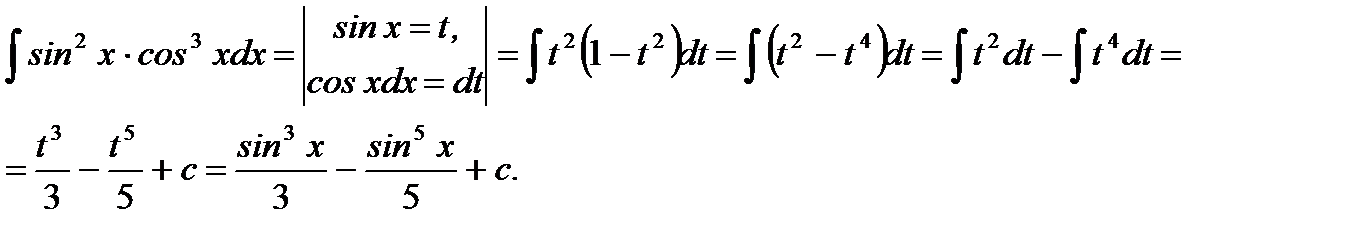
Ответ: 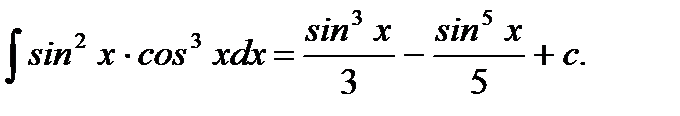
Пример 5.31.Вычислить неопределенный интеграл 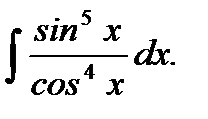
Решение.
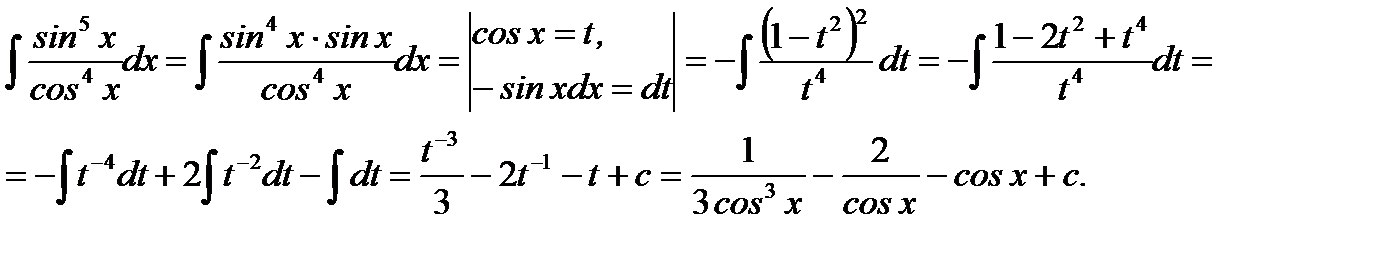
Ответ: 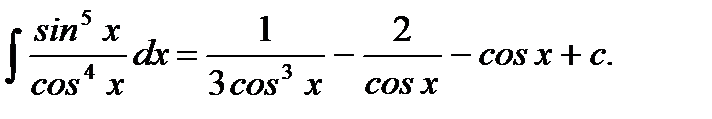
Пример 5.32.Вычислить неопределенный интеграл 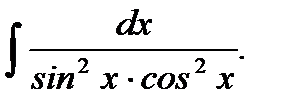
Решение.
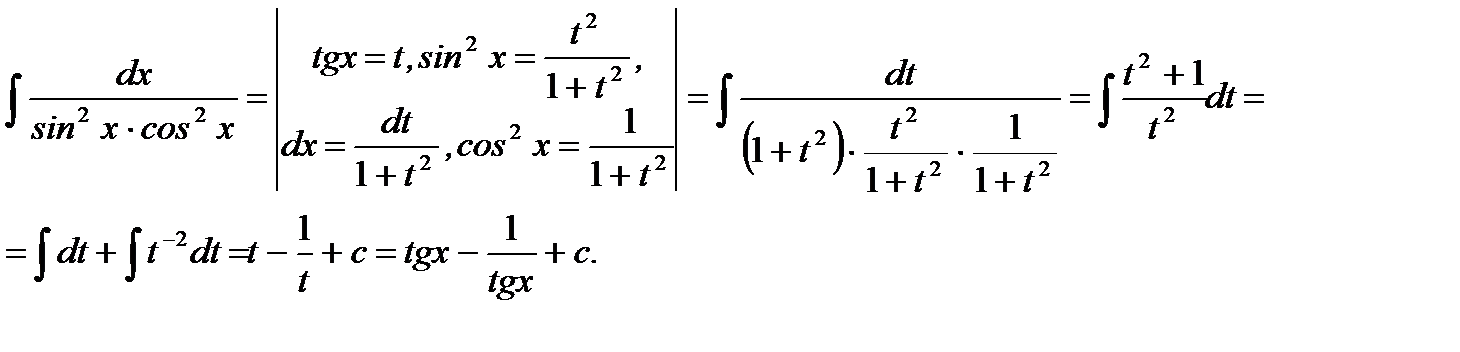
Ответ: 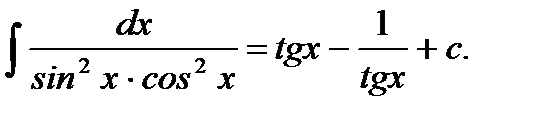
Пример 5.33.Вычислить неопределенный интеграл 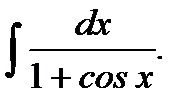
Решение.
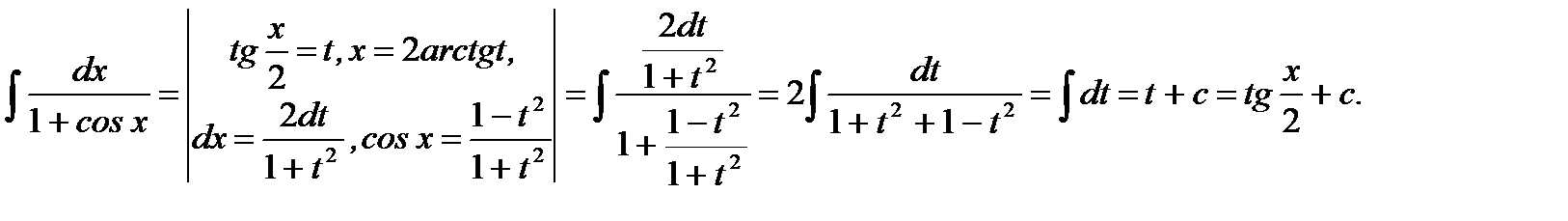
Ответ: 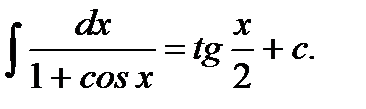
Определенный интеграл и его применение.
Дата добавления: 2021-05-28; просмотров: 646;











