Метод интегрирования по частям

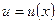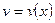Пусть и - непрерывно дифференцируемые функции. На основании формулы дифференциала произведения имеем

.

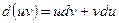Отсюда

.

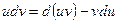Интегрируя, получим:

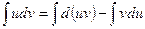или окончательно

.

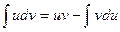(4)

Формула (4) называется формулой интегрирования по частям.

Выведенная формула показывает, что интеграл 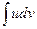приводится к интегралу 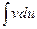, который может оказаться более простым, чем исходный, или даже табличным. Сущность метода интегрирования по частям вполне соответствует его названию. Дело в том, что при вычислении интеграла этим методом подынтегральное выражение 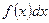представляется в виде произведения множителей u и dv. При этом dx обязательно входит в dv. В результате получается, что заданный интеграл находится по частям: сначала находим 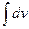, а затем .

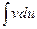Пример 1.

.

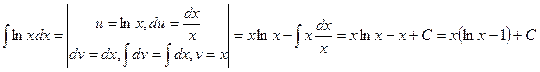В представленном примере, как и в дальнейших, вертикальными черточками отделены вспомогательные записи. Отметим также, что в качестве v можно взять любую функцию вида x+C, где С – постоянная. Мы взяли v=x, т.е. С=0.

Пример 2. .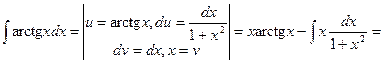

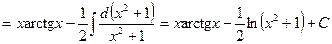Пример 3.

.

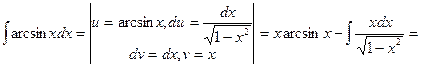
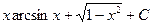Пример 4.

.

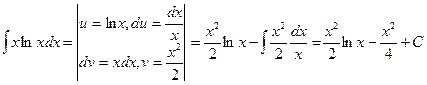Иногда для вычисления интеграла формулу интегрирования по частям приходится применять несколько раз.

Пример 5.

.

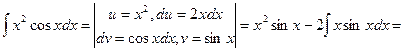
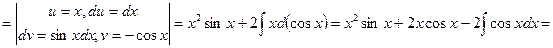
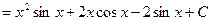Таким образом, интеграл 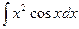вычислен двукратным интегрированием по частям.

Пример 6.

.

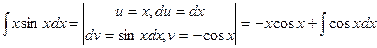
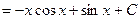Если бы выражение u и dv мы выбрали иначе, т.е. 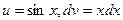, то получили бы 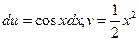, откуда 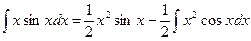, и пришли бы к интегралу более сложному, чем исходный, т.к. степень сомножителя при тригонометрической функции повысилась на единицу.

Приведенный пример показывает, что при вычислении интегралов методом интегрирования по частям главным является разумное разбиение подынтегрального выражения на множители u и dv. Общих установок по этому вопросу не имеется. Однако, для некоторых типов интегралов сделать это возможно.

а) В интегралах вида

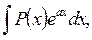
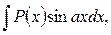
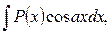
где P(х) – многочлен относительно x, а – некоторое число, полагают u=P(x), а остальные сомножители за .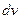

Пример 7. Найти .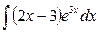

D Положим 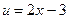, , 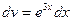тогда 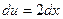, 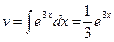. Следовательно,

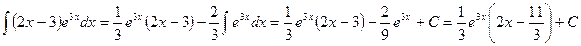Ñ

б) В интегралах вида

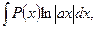
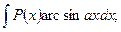
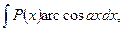
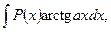
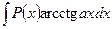
полагают 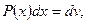а остальные сомножители – за u.

Пример 8. Найти .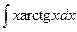

D Положим 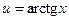, , 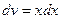тогда , .

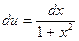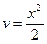Следовательно, .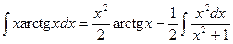

Вычислим отдельно последний интеграл:

.

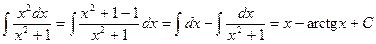Итак, 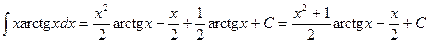. Ñ

Отметим, что на практике важно научиться применять формулу (4), не выписывая по возможности в стороне выражения для функций u и v.

Так, решение приведенного примера может быть представлено в виде:

D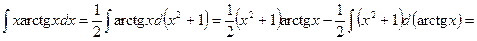

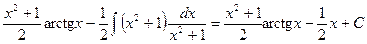= . Ñ