Математика пучка прямых.

Если бы полупроводниковые диоды обладали ВАХ в виде идеальных экспонент, то семейство ВАХ в зависимости от температуры могли бы выглядеть в виде сужающегося пучка прямых. Рассмотрим математику пучка прямых по формуле

Ln(Ia) = K_T∙ ( T∙ (U_F -Ua) + T_F∙ (Ua-U_B) ) (7.04) ;

Для диода КД 213А коэффициенты имеют следующие величины:

K_T = 0,0956 В^-1 ∙ К^-1; T_F =605,2 K; U_B = 0,885 В; U_F = 1,161В.

Рассмотрим 1-й вариант.

Рассмотрим уравнение (7.04) для пучка прямых, если аргументом является Ua. Это и есть семейство ВАХ диода в зависимости от температуры. На рис. 1 показан такой пучок прямых.

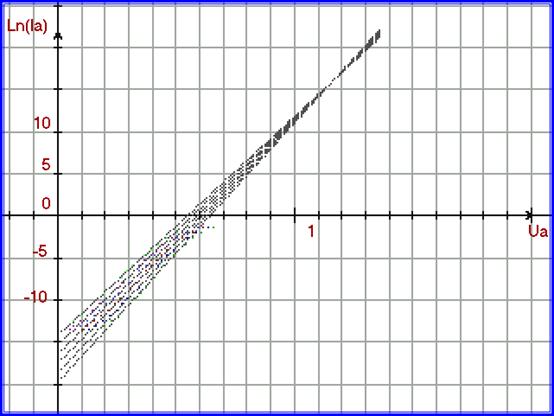
Рис. 1. Иллюстрация совпадения пучка прямых по формуле (7.04) и 2-го участка экспериментальных данных для диода КД213А. Графики построены в полулогарифмическом масштабе.

Прямые пучка пересекаются в точке фокуса, аргумент которой равен:

Ua = U_F

Для КД213А Ua = U_F = 1,161 В.

При Ua = U_F , согласно уравнению (7.04), температура престаёт оказывать влияние на Ia. Ln(Ia) в этой точке всегда равен одной и той же величине, независимо от температуры. Величина этого тока равна:

Ln(I_F) = K_T ∙ T_F ∙ ( U_F - U_B )

После точки фокуса, далее, при росте Ua, действие температуры на ток меняется на противоположное, и увеличение температуры вызывает уменьшение тока. Этим свойством обладает выражение (7.04). Температурный коэффициент вдруг меняется на противоположный. Ну а величина этого коэффициента зависит от величины Ua.

Рассмотрим 2-й вариант.

Рассмотрим уравнение (7.04) для пучка прямых, если аргументом является температура.

Согласно уравнению (7.04) построим график Ln(Ia) в зависимости от температуры.

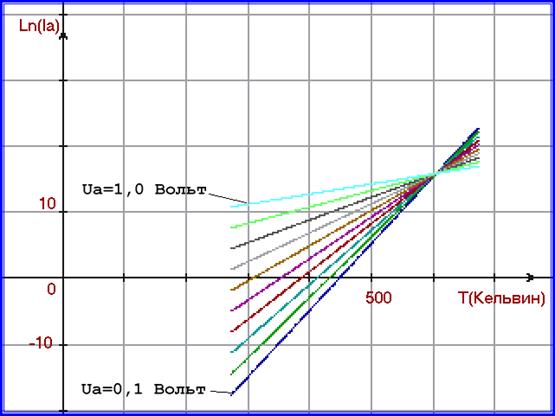
Рис. 2 Зависимость Ln(Ia) от температуры для диода КД213А по формуле (7.04) .

На рисунке 2 приведены графики функции (7.04) при

Ua = 0,1 В.;

Ua = 0,2 В.;

Ua = 0,3 В.;

Ua = 0,4 В.;

Ua = 0,5 В.;

Ua = 0,6 В.;

Ua = 0,7 В.;

Ua = 0,8 В.;

Ua = 0,9 В.;

Ua = 1,0 В.

Крайние значения для Ua на рисунке 2 обозначены.

Наблюдая рисунок 2, заметим, что прямые пучка пересекаются в точке фокуса при определённой температуре:

T = T_F ;

Для КД213А T_F = 605,2 К.

При T = T_F , согласно уравнению (7.04), напряжение Ua престаёт оказывать влияние на Ia. Ln(Ia) в этой точке всегда равен одной и той же величине, независимо от напряжения Ua. Величина натурального логарифма этого тока равна:

Ln(I_F) = K_T ∙ T_F ∙ ( U_F - U_B )

Можно сделать вывод, что для уравнения

Ln(Ia) = K_T ∙ ( T∙ (U_F -Ua) + T_F ∙ (Ua-U_B) ) (7.04) ;

K_T = 0,0956 Вольт^-1 ∙ Кельвин^-1 - коэффициент;

T_F =605,2 Kельвин - температура фокуса для аргумента T;

U_B = 0,885 Вольт - напряжение электрического барьера ;

U_F = 1,161Вольт - напряжение фокуса для аргумента Ua;

U_F = U_B + U_D ,

U_F - U_B = U_D - разность потенциалов,

влияющая на величину Ln(I_F) = K_T ∙ T_F ∙ ( U_F - U_B ).

Мы рассмотрели математику эмиссионного уравнения (7.04) и определили свойства параметров T_F и U_F.

ПРИЛОЖЕНИЕ 6