Реостатный принцип усиления. Влияние сопротивления нагрузки на выходное напряжение.

Моделью транзисторного или лампового усилителя является переменное управляемое сопротивление. Такую модель можно создать на основе схемы реостата и на основе схемы потенциометра. На рисунке 1 приведена схема транзисторного усилителя, моделируемого переменным резистором по схеме реостата.

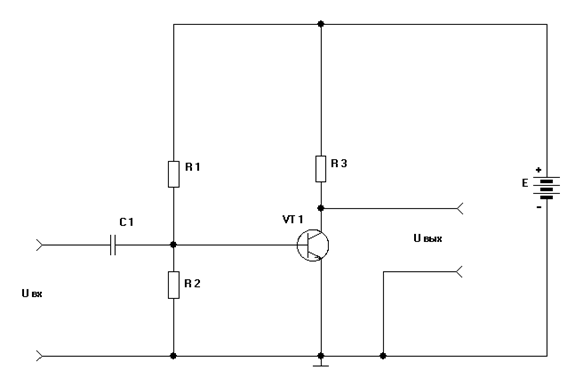
Рис. 1. Схема транзисторного усилителя, моделируемого переменным резистором по схеме реостата.

На рисунке 1 резистор R3 является нагрузочным, транзистор VT 1 является управляемым элементом. Для получения математической модели, заменим транзистор переменным резистором по схеме реостата.

Рассмотрим модель усилителя, моделируемую переменным резистором по схеме реостата. Схема модели приведена на рисунке 2.

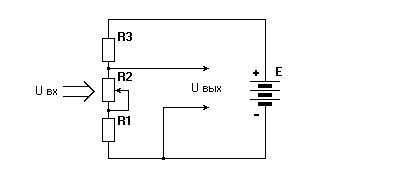
Рис. 2. Схема модели.

На рисунке 2 показана схема модели на основе реостата.

На рисунке 2 обозначены:

R1 – минимальное сопротивление управляемого элемента.

R1 = n ;

R1+R2 – максимальное сопротивление управляемого элемента.

R1+R2 = m ;

R3 – сопротивление нагрузки. R3 = k ;

E – напряжение источника питания.

Движок резистора двигается вверх и вниз с некоторой частотой, что соответствует изменению сопротивления управляемого элемента (в данном случае это может быть сопротивление между выводами коллектора и эмиттера транзистора VT 1 на рис. 1.)

Поставим задачу:

Какую величину резистора R3 надо выбрать таким образом, чтобы изменение выходного напряжения было наибольшим, при изменении сопротивления управляемого элемента от R1 до R1+R2.

Решение:

Рассмотрим 2 схемы модели данного усилителя для двух крайних положений резистора R2.

Рис. 3. Схема для верхнего положения движка переменного резистора.

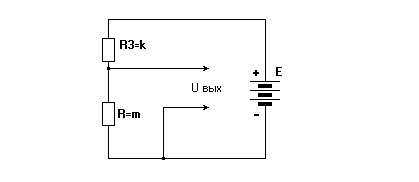
Рис. 4. Схема для нижнего положения движка переменного резистора.

Для схемы на рис. 3. имеем:

I макс = E / ( k + n) ;

U мин = E∙n / ( k + n) ;

Для схемы на рис. 4. имеем:

I мин = E / ( k + m) ;

U макс = E∙m / ( k + m) ;

Находим разность ∆U = U макс – U мин.

∆U = U макс – U мин = E∙m / ( k + m) - E∙n / ( k + n) ;

∆U = ( E∙ (m-n) ∙k ) / ( ( k+n ) ∙ ( k+m ) ) ;

Исследуем функцию ∆U на максимум относительно переменной k.

∆U = E ∙ F(k) ;

( k+n ) ∙ ( k+m ) ∙ ( m-n ) – ( m-n ) ∙k∙ (2∙k+n+m)

F(k)′ = ---------------------------------------------------------------

( k+n )² ∙ ( k+m )²

( m-n ) ∙ ( m∙n – k² )

F(k)′ = ---------------------------

( k+n )² ∙ ( k+m )²

Найдём экстремум функции. Для этого найдём значение k, при котором F(k)’ = 0.

( m-n ) ∙ ( m∙n – k² )

F(k)′ = --------------------------- = 0

( k+n )² ∙ ( k+m )²

Находим:

k² = n∙m

k+n ≠ 0

k+m ≠ 0

_____

k = √ m∙n

Решение:

Оптимальным значением R3 ( на рис. 2. ) – резистора нагрузки, обеспечивающим максимальное выходное напряжение, является значение:

_____

k = √ m∙n - среднее геометрическое от максимального и минимального сопротивления управляемого элемента.

На рисунке 5 приведён график зависимости выходного напряжения от нагрузочного резистора при E=10 Вольт, n = 100 Ом,

m = 10000 Ом. Максимум кривой определяется следующим значением для k:

_____ __________

k = √ m∙n = √ 100∙10000 = 1000 Ом

Рис. 5. График зависимости выходного напряжения от нагрузочного резистора при E=10 Вольт, n = 100 Ом, m = 10000 Ом.

Теперь, когда задача была решена, то необходимо найти математические модели для вольт-амперных характеристик электронных приборов: ламповых усилительных ламп, и для транзисторов.