Релаксация электрической энергии при разряде конденсатора на резистор.

Вывод закона релаксации электрической энергии при разряде конденсатора на резистор.

В качестве вывода закона релаксации, приведём часть § 74 из книги С.Г. Калашникова «Электричество».

§ 74. Конденсатор в цепи с сопротивлением

В качестве примера квазистационариых токов рассмотрим процессы зарядки и разрядки конденсатора. Пусть конденсатор с емкостью С включен в схему рис. 106

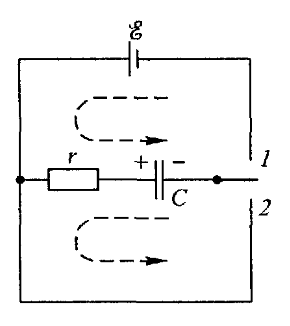
Рис 106 Заряжение и разряжение конденсатора.

Тогда, ставя переклю­чатель в положение 1, мы будем заряжать конденсатор от ис­точника тока, а перебрасывая переключатель в положение 2, — разряжать конденсатор

Рассмотрим сначала процесс зарядки конденсатора Обозна­чим через E ЭДС источника, через r — сопротивление цепи (включая и внутреннее сопротивление источника) и выберем положительное направление тока, как показано на ри­сунке. Применяя к контуру ErCE вто­рое правило Кирхгофа, получим

здесь i — мгновенное значение силы то­ка, U — мгновенное значение напряже­ния на конденсаторе. Но

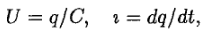
где q — заряд конденсатора. Из напи­санных трех равенств мы можем исклю­чить две из трех переменных величин q,i и U и получить уравнение для какой-либо одной из них Ис­ключая q и i , находим

Мы получили для определения U дифференциальное уравнение первого порядка с постоянными коэффициентами Введем новую переменную и = U —E Тогда

В этом уравнении переменные разделяются, и в результате ин­тегрирования находим

Постоянная интегрирования А зависит от начального усло­вия. Положим, что мы начинаем отсчет времени с момента за­мыкания переключателя. Тогда начальное условие имеет вид

Это даёт

Возвращаясь к прежней переменной U, находим окончательно для напряжения на конденсаторе выражение

При t = 0 это выражение дает U = 0 в соответствии с началь­ным условием задачи. С увеличением времени t напряжение U непрерывно увеличивается и асимптотически приближается к ЭДС источника.

Зависимость зарядного тока от времени имеет вид

Сила тока имеет наибольшее значение в начальный момент вре­мени и асимптотически стремится к нулю в процессе зарядки.

В случае разрядки конденсатора исходные уравнения будут

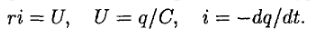
В отличие от предыдущего, в выражение для тока i входит знак минус, так как выбранное нами положительное направление то­ка соответствует уменьшению заряда конденсатора. Исключая из написанных равенств q и i, получим

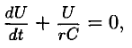
откуда

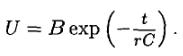
Если начало отсчета времени совпадает с началом процесса раз­рядки, то начальное условие будет

В этом случае постоянная интегрирования равна В = E и зависимость напряжения конденсатора от времени имеет вид

Полученные результаты показывают, что процессы заряже­ния и разряжения (установление электрического равновесия) происходят не мгновенно, а с конечной быстротой. Для рас­смотренного контура, содержащего сопротивление и емкость, быстрота установления зависит от произведения

которое имеет размерность времени и называется постоянной времени данного контура. Постоянная времени показывает, че­рез какое время после выключения ЭДС напряжение (а значит, и напряженность поля внутри конденсатора) уменьшается в e = 2,71 раза. Если r и С выражать в единицах системы СИ (в омах и фарадах), то Т будет выражено в секундах. Мы полу­чим Т в секундах и в том случае, если будем выражать r и С в единицах системы СГС, так как в обеих этих системах единицей времени служит секунда.