Термоэлектронная эмиссия P-N перехода при протекании прямого тока в кремниевом диоде КД213А.

Объяснить принцип работы полупроводникового диода можно, рассмотрев эмиссионное уравнение и особенности его составных частей. Так, как основное уравнение, описываемое выражением:

Ln(Ia) = K_T ∙ ( ( T_F - T ) ∙ (Ua - U_B) + T ∙ U_D )

совпадает по форме с эмиссионным уравнением электровакуумного диода, то можно сказать, что явления однонаправленных токов в том и другом случае - родственные.

Разница заключается в различном написании уравнений для T_F и U_B .

Изотоковые характеристики полупроводникового кремниевого диода КД213А.

На рисунке 3 выразим экспериментальные данные в виде изотоковых кельвин-вольтовых характеристик.

Рис. 3. 20 изотоковых характеристик ( 20 токов ) для 6-ти температур – 10,20,30,40,50,60 градусов по Цельсию. Изотоковые характеристики были вычислены из экспериментальных данных.

На рис. 3 приведены характеристики для следующих стабильных токов:

1,3 мкА,

2,2 мкА,

4,0 мкА,

7,6 мкА,

14,3 мкА,

27,8 мкА,

52,2 мкА,

101,4 мкА,

199,2 мкА,

377,3 мкА,

724 мкА,

1,371 мА,

2.66 мА,

4,98 мА,

9,31 мА,

18,67 мА,

35,77 мА,

70,2 мА,

143,5 мА,

254,9 мА,

На рис. 3 они располагаются снизу вверх в порядке возрастания.

С помощью эмиссионного уравнения на рисунке 4 построим математическую модель 3-х изотоковых характеристик для

Ia = 1,3 мкА, Ia = 377,3 мкА, Ia = 254,9 мА поверх точек экспериментальных данных.

Рис. 4. Математические модели 3-х изотоковых характеристик для кремниевого полупроводникового диода КД213А.

На рисунке 4 можно наблюдать, что график математической модели для тока 1,3 мкА проходит немного ниже, чем соответствующие экспериментальные данные. Это обусловлено влиянием на эксперимент шунтирующего сопротивления Rs = 210267 Ом на

PN-переход.

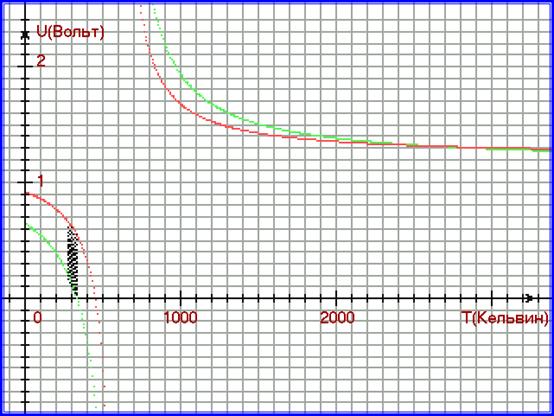
Рис. 5. Математические модели 2-х изотоковых характеристик для кремниевого полупроводникового диода КД213А.

На рисунке 5 построим математическую модель изотоковых характеристик так, чтобы можно было наблюдать обе ветви гиперболы. Математические модели построены для токов Ia = 1,3 мкА и

Ia = 250 мА , тёмными точками построены изотоковые характеристики (из-за крупного масштаба, они плохо различимы и похожи на вертикальный параллелограмм).

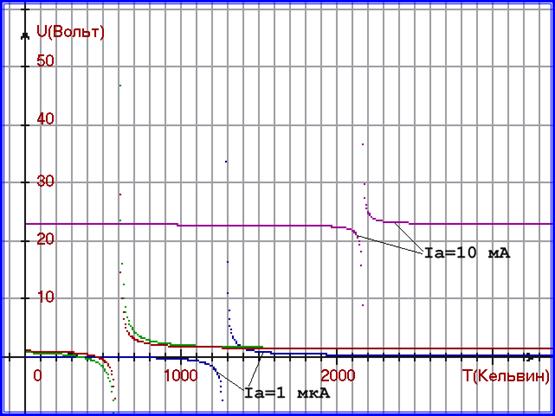
Рис. 6. Математические модели 2-х изотоковых характеристик для кремниевого полупроводникового диода КД213А и математические модели 2-х изотоковых характеристик для электровакуумного диода эксперимента С. Дэшмана.

Изменим масштаб и на рисунке 6 к уже имеющимся 2-м изотоковым характеристикам кремниевого полупроводникового диода, построим ещё 2 математические модели изотоковых характеристик для электровакуумного диода эксперимента С. Дэшмана: построим для Ia = 1 мкА, и для Ia = 10 мА.

Следует учесть, что для полупроводникового диода изотоковые характеристики строятся на левой ветви гиперболы, а для вакуумного диода - на правой. На рисунке 6 можно наблюдать различия в математических моделей вакуумного и полупроводникового диода.

Вывод.

Эмиссионное уравнение - это объединяющее уравнение для термодинамики и электродинамики при исследовании токов, протекающих через две (и более) среды.

Между тем, как квантовые законы – формула Шокли и закон Ричардсона-Дэшмана неверно описывают соответствующие им физические явления.

ПРИЛОЖЕНИЕ 7