Математика процессов обратных связей. ООС. ПОС.

Обратные связи – взаимодействие сигналов во времени. Практическим способом обратные связи были обнаружены в усилительных устройствах. Оказалось, что полярность сигнала – направление его роста во времени играет определяющую роль при сложении входных и выходных сигналов.

Полярность входного сигнала берётся за основу. Если представить такой входной сигнал как линейно возрастающий (на практике - пилообразный), то на выходе мы можем иметь два варианта полярности этого сигнала: линейно возрастающий во времени, линейно убывающий во времени.

Создавая обратную связь, часть выходного сигнала подаём на вход. Здесь мы замечаем, что сигналы электронных усилителей распространяются мгновенно. Они взаимодействуют во времени согласно математическим уравнениям обратной связи. Причём полярность поданного с выхода на вход сигнала определяет Отрицательную Обратную Связь (в нашем случае: линейно убывающий сигнал) и Положительную Обратную Связь (в нашем случае: линейно возрастающий сигнал).

Казалось бы, полярность сигнала определяет свойства объектов пространства. Но возникает взаимодействие пространства во времени.

Алгоритм такого взаимодействия для линейно возрастающего сигнала, при ПОС:

1.Входной сигнал растёт.

2. Выходной сигнал имеет большую величину, чем входной.

3. Таким образом: Выходной сигнал – это «будущее» для входного.

При включении положительной обратной связи мы имеем попытку совершить путешествие во времени из настоящего в будущее. Чем закончиться такая попытка? Мы знаем, что ПОС – это нестабильное состояние, сопровождающееся ГЕНЕРАЦИЕЙ сигнала. В природе ПОС можно идентифицировать с такими явлениями как многократные зеркальные отражения.

Если встать между параллельными плоскими зеркалами, направленными навстречу друг другу, можно увидеть многократные зеркальные отражения. Если между зеркалами создать маленький угол, то количество отражений будет конечным. Также явление многократных отражений сопутствует явлению генерации лазерного луча. То есть различного рода автогенераторы, лазеры – всё это попытки совершить путешествие в будущее.

Алгоритм такого взаимодействия для линейно возрастающего сигнала при ООС:

1.Входной сигнал растёт.

2. Выходной сигнал имеет меньшую величину, чем входной.

3. Таким образом: Выходной сигнал – это «прошлое» для входного.

При включении отрицательной обратной связи мы имеем попытку совершить путешествие во времени из настоящего в прошлое. Чем закончиться такая попытка? Мы знаем, что ООС – это стабильное состояние, сопровождающееся ОГРАНИЧЕНИЕМ.

В фантастическом рассказе «И грянул гром.» Рэя Брэдбери говориться как раз о путешествии в прошлое. Там происходит изменение мира будущего из-за гибели одной бабочки в мире прошлого.

Но в усилителе с ООС происходит ОГРАНИЧЕНИЕ. То есть, «Эффект бабочки» в этом мире недостижим из-за свойства пространства и времени создавать ООС – некоторое ОГРАНИЧЕНИЕ, преодолеть которое невозможно.

Об ООС ещё говорят как о стабилизации.

Наблюдая обратные связи, мы наблюдаем два явления: одно нестабильное, приводящее к ГЕНЕРАЦИИ колебаний (ПОС) , второе более стабильное, чем обычно из-за процесса САМООГРАНИЧЕНИЯ (ООС).

Электрические сигналы пытаются путешествовать во времени. Как мы знаем, что электрические сигналы измеряются в ваттах и имеют вид тепловых потоков. Увеличивая мощность экспериментальных установок, работающих с ПОС и ООС можно построить машину времени… Но это произойдёт в том случае, если пространство и время сдадут свои позиции.

Рассмотрим математические модели обратных связей. В математике функции с обратными связями называют неявными функциями.

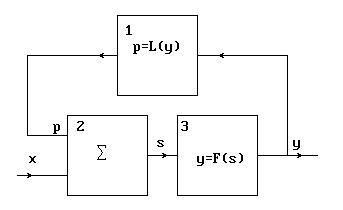
Рис. 1.27. Блок-схема системы с обратной связью.

На рисунке 1.27. приведена блок-схема системы с обратной связью.

На рис. 1.27. обозначены:

1 - блок функции обратной связи;

2 - блок сумматора;

3 - блок функции прямой связи;

x - входной сигнал; s - промежуточный; p - сигнал обратной связи;

y - выходной сигнал;

p=L(y) - функция обратной передачи;

y=F(s) - функция прямой передачи.

Для различных функций y=F(s): для линейной, степенной, экспо -ненциальной можно создать системы с обратными связями, а также вычислить решения для обратных связей, применяя аналитические формулы или алгоритмы.