Взаимное расположение прямых. Скрещивающиеся прямые.

Стереометрия. Основные понятия. Аксиомы стереометрии

Стереометрия – раздел геометрии, в котором изучаются свойства фигур в пространстве.

Введение в стереометрии нового неопределяемого понятия – «плоскость» приводит к расширению системы аксиом. Рассмотрим группу аксиом, которая выражает основные свойства плоскости.

· Какова бы ни была плоскость, существуют точки принадлежащие этой плоскости и точки, ей не принадлежащие.

· Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку

· Если две различные прямые имеют общую точку, то через них можно провести плоскость и притом только одну.

Замечание: содержание аксиом в группе можно изменять, например, третью аксиому можно заменить аксиомой «через точку и не лежащую на ней прямую проходит плоскость и притом только одна», в этом случае утверждение «Если две различные прямые имеют общую точку, то через них можно провести плоскость и притом только одну» станет теоремой и потребует доказательства.

Следствия из аксиом

Следствие 1: Через прямую и не лежащую на ней точку можно провести плоскость и притом только одну

Следствие 2: Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости

Следствие 3: Через три точки, не лежащие на одной прямой, можно провести плоскость и притом только одну

Примем эти теоремы без доказательств.

Взаимное расположение прямых. Скрещивающиеся прямые.

Две прямые в пространстве называются пересекающимися, если они лежат в одной плоскости и имеют только одну общую точку

Напомним, что две прямые совпадают, если они имеют по крайней мере две общих точки

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются

Прямые, которые не лежат в одной плоскости называются скрещивающимися

Замечание: для двух прямых возможно одно и только одно из четырех расположений: они могут либо совпадать, либо пересекаться, либо скрещиваться, либо быть параллельными.

Теорема: Через точку вне данной прямой можно провести прямую, параллельную данной, и притом только одну.

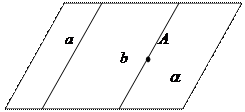Доказательство: пусть а – данная прямая, А – точка, не лежащая на ней. Докажем, что существует единственная прямая b параллельная а, такая что АÎb.

Проведем через прямую а и точку А плоскость a,

Проведем через точку А в плоскости a прямую b//a.

Покажем, что эта прямая единственна. Допустим, что существует с//а и АÎс.

Тогда через прямые b и с можно провести плоскость b. Плоскость b проходит через прямую а и точку А, следовательно, по следствию 1 из аксиом плоскости она единственна, т.е. совпадает с a. Но в плоскости через точку не лежащую на прямой проходит только одна прямая параллельная данной, т.е. прямые b и с совпадают.

Теорема: Две прямые, параллельные третьей, параллельны между собой

Доказательство:Пусть b//a, c//a. Докажем, что b//c. Рассмотрим случай, когда a,b,c не лежат в одной плоскости. Пусть b- плоскость, в которой лежат прямые a и b, g - плоскость, в которой лежат прямые а и с. Плоскости b и g различны( почему?

)

Отметим на прямой b точку B и проведем плоскость g₁ через прямую с и точку В. Она пересечет плоскость b по прямой b₁. Прямая b₁ не перескает плоскость g. Действительно, точка пересечения должна принадлежать прямой а, т.к b₁ лежит в плоскости b. С другой стороны, она должна лежать и на прямой с, т.к. b₁Îg₁, но прямые а и с не пересекаются. Т.к. b1Îb и не пересекает аÎb то они параллельны, а значит b1 совпадает с b. Т.о., b совпадая с b1 лежит в одной плоскости с с – в g₁ и не пересекает ее. Значит, b//c.

Теорема(признак скрещивающихся прямых): Если одна из двух прямых лежит в некоторой плоскости, а другая пересекает эту плоскость в точке, не принадлежащей первой прямой, то эти прямые – скрещивающиеся

Доказательство: самостоятельно

Теорема: Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

Доказательство: самостоятельно.

12 3

Дата добавления: 2021-12-14; просмотров: 431;