Двухмерный процессовый переход. Общее уравнение для функции процессового перехода. Внешняя функция процессового перехода.

Если функциональные зависимости A и B будут зависеть каждая от своей переменной, то такой процессовый переход мы назовём двухмерным. Схема для такого варианта – двухмерного процессового перехода приведена на рисунке 5.3.

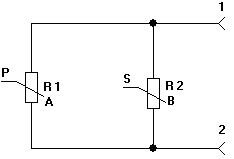
Рис. 5.3. Схема для 2-х параллельно соединённых резисторов, функционально зависимых (по разным функциям : A и B) от разных параметров ( двух переменных P и S).

На практике такая схема выглядела бы так:

Резистором R1 управляет тепловой поток: R1- это терморезистор.

Резистором R2управляет световой поток R2- это фоторезистор.

Такая схема бессмысленна с точки зрения практической радиоэлектроники, но мы пытаемся создать теорию математических моделей, способных объединять 2 процесса. С этой точки зрения, схема имеет смысл. Система уравнений будет следующая:

A = F1(P) ;

B = F2(S).

Rрез = -----------------

1 1

--- + ---

A B

Сформулируем общий случай уравнения «весов». Выразим через переменные x, y, z. y – обозначим функцию, x и z – два аргумента.

Система уравнений «весов» имеет вид:

y = A = F1(x)

y = B = F2(z)

y_рез = -----------------

1 1

--- + ---

A B

Преобразуем:

A∙B

y_рез = ------------ (5.2.3.,01)

A + B

В уравнении (5.2.3.,01) можно увидеть механизм сравнения – «взвешивания» функций A и B. При значении А стремящемуся к значению много большему чем B, y_рез стремиться к значению B. Приведём наглядный графический пример. Рассмотрим одномерный процессовый переход (см. рис. 5.4.):

y = A = F1(x) = x²

y = B = F2 (x) = 0,2 ∙ x + 50

A∙B

y_рез = ----------

A + B

Наблюдения показывают, что процессовый переход можно сделать на каком-то участке аргумента. Функции A и B должны быть монотонны.

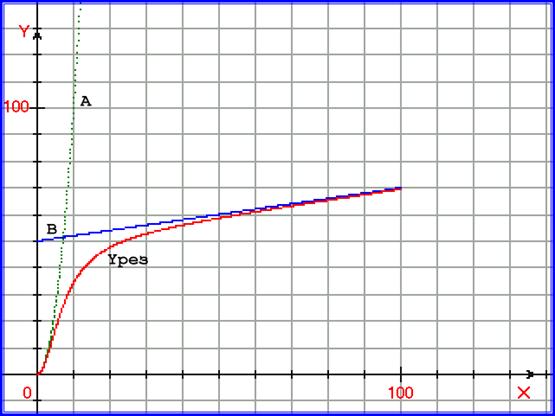
Рис. 5.4. График, иллюстрирующий одномерный процессовый переход. На графике построены функция y=A = x² , функция y = B= 0,2∙x+50, а также функция y_рез =A∙B/(A+B) .

Кривизну перехода от А к B необходимо каким-то образом регулировать. Плавность изгиба переходного участка между A и B можно регулировать, если применить метод, использующий прямые и обратные монотонные возрастающие функции.

Например: функция y = F(x) - монотонная, возрастающая функция.

__

Тогда обратная функция: x = F (x)

Система уравнений «весов» с использованием нового метода будет выглядеть так:

y = A = F1(x)

y = B = F2 (x)

__

y_рез = A∙B / F ( F( A) + F( B) ) (5.2.3.,02)

В таком случае функция F будет называться внешней, а функции A и B – внутренними.