Поверхности вращения

Проецирование геометрических фигур

Геометрическая фигура – это любое множество точек, которое может состоять из нескольких точек или бесконечного числа точек.

В НГ фигуры отображаются на плоскость с помощью проецирования.

Способы проецирования

1. Центральное.

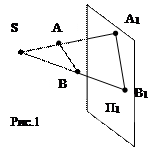
Аппарат проецирования: т.S – центр проецирования, П₁ – плоскость проекций.

Для получения проекции т.А на пл. П₁ через т.S проводят проецирующую прямую(луч) SA до пересечения с П₁ (рис.1). Точка А₁ – это центральная проекция точки А.

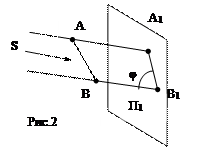
2. Параллельное– т.S удаляется в ∞, поэтому проецирующие лучи параллельны (рис.2).

Аппарат проецирования: S – направление проецирования, П₁ – плоскость проекций.

Виды параллельного проецирования (в зависимости от угла проецирования)

2.1. Прямоугольное (ортогональное) – угол φ =90˚.

2.2. Косоугольное – φ <> 90˚.

Свойства прямоугольного проецирования

1. Проекции параллельных прямых параллельны.

2. Проекции равных и параллельных отрезков равны и параллельны.

3. Проекция точки делит проекцию отрезка в таком же соотношении, в каком точка делит отрезок.

Т. А будет соответствовать единственная проекция А₁ , т.к. проецирующая прямая пересекает П₁ только в одной точке. Однако восстановить точку А только по одной проекции нельзя, т.к. любая точка лежащая на проецирующей прямой является проекцией А_1. Поэтому для получения обратимого чертежа геометрической фигуры необходимо иметь две проекции.

Метод Монжа

При разработке чертежей конструкторской документации применяется проекционная модель Монжа.

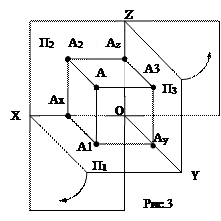Сущность метода: ортогональное проецирование геометрических фигур на две или три взаимно перпендикулярные плоскости (рис.3):

- П₁ – горизонтальная плоскость проекций;

- П₂ – фронтальная плоскость проекций;

- П₃ – профильная плоскость проекций.

Плоскости безграничны и делят пространство на 8 частей -октантов, отсчет которых ведется по часовой стрелке, если смотреть по положительному направлению оси Х.

Проекции точки

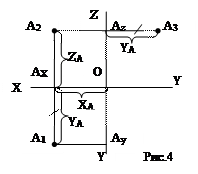Пусть в некоторой системе трех взаимно перпендикулярных плоскостей дана т. А. Для построения ортогональных проекций А₁, А₂, А₃ через т. А проводят прямые, перпендикулярные плоскостям проекций П₁, П₂, П₃, и определяются точки пересечения этих перпендикуляров с плоскостями проекций:

А₁ – горизонтальная проекция т. А (А₁=А А₁ ∩ П₁ );

А₂ – фронтальная проекция т. А (А₂=А А₂ ∩ П₂ );

А₃ – профильная проекция т. А (А₃=А А₃ ∩ П₃ );

От пространственного изображения т. А переходят к комплексному чертежу (эпюру).

Эпюр Монжа получается путем совмещения плоскостей проекций П₁ и П₃ с неподвижной фронтальной плоскостью П₂ , а именно вращением П₁ вокруг ОХ и П₃ вокруг ОZ (рис.4).

Прямая А₁ А_х А₂ - вертикальная линия связи, А₂ А_z А₃ - горизонтальная линия связи.

Для того, чтобы однозначно определить положение точки в пространстве достаточно две проекции, третью всегда можно достроить, т.к. А₁ А_х = А_z А₃.

Координатами X, Y, Z точки называются числа выражающие её расстояния до плоскостей проекций: X – до профильной, Y – до фронтальной, Z – до горизонтальной. Зная координаты точки, можно построить ее проекции на комплексном чертеже.

Проекции прямых

В зависимости от положения относительно плоскостей проекций прямые делятся на:

1) прямые общего положения – это прямая, наклоненная ко всем плоскостям проекций (рис.5,6);

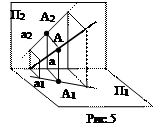
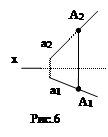Условие принадлежности точки прямой: если точка принадлежит прямой, то проекции точки принадлежат одноименным проекциям прямой (А₁ Î а₁, А₂ Î а₂).

2) прямые частного положения:

2.1) уровня – параллельные одной из плоскостей проекций;

- горизонталь - ║ П₁ (h₂ ║ ОХ) (рис.7);

- фронталь - ║ П₂ (f₁ ║ ОХ) (рис.8);

- профильная прямая - ║ П₁ (p₁ ║ ОY , p₂ ║ ОZ) (рис.9).

2.1) проецирующие – перпендикулярные одной из плоскостей проекций:

- горизонтально -проецирующая прямая(рис.10);

-
фронтально -проецирующая прямая(рис.11);

- профильно-проецирующая прямая(рис.12);

В зависимости от положения в пространстве относительно друг друга прямые делятся на:

1) 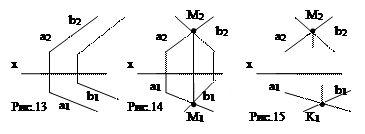параллельные – одноименные проекции прямых взаимно параллельны: a₁

2)

3)

4)

5)

6)

7)

8) ║ b₁ , a₂ ║ b₂ (рис.13);

9) пересекающиеся – проекции прямых пересекаются в точках, лежащих на одной линии связи: a₁ ∩ b₁ = M₁, a₂ ∩ b₂ = M₂ (рис.14);

10) скрещивающиеся – не параллельны и не пересекаются (рис.15).

Проекции плоскости

Способы задания плоскости:

1. Три точки, не лежащие на одной прямой.

2. Прямой и точкой, не принадлежащей этой прямой.

3. Двумя параллельными прямыми.

4. Двумя пересекающимися прямыми.

5. Плоской фигурой (треугольник, окружность и т.д.).

В зависимости от положения относительно плоскостей проекций плоскости делятся на:

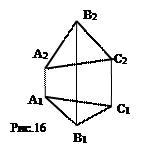
1) плоскости общего положения (рис.16);

Условие принадлежности точки плоскости: точка принадлежит плоскости, если она принадлежит какой-либо прямой этой плоскости.

2) плоскости частного положения:

2.1) проецирующие

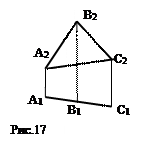
- горизонтально – проецирующая плоскость ∆ ABC ┴ П₁ (рис.17);

- фронтально - проецирующая плоскость ∆ ABC ┴ П₂;

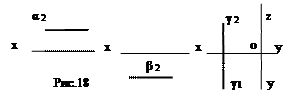- профильно- проецирующая плоскость ∆ ABC ┴ П₃.

2.1) уровня (рис.18);:

- горизонтальная плоскость уровня α║П₁

- фронтальная плоскость уровня β ║П₂;

- профильная плоскость уровня γ ║П₃.

Условие принадлежности прямой плоскости: прямая принадлежит плоскости, если она проходит:

а) через две точки, принадлежащие этой плоскости;

б) через одну точку, принадлежащую плоскости, и параллельно прямой, принадлежащей плоскости.

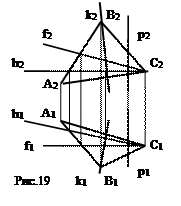Главные линии плоскости (рис.19) – горизонталь – h (h Î ∆ ABC), фронталь – f (f Î ∆ ABC), профильная прямая – p (p Î ∆ ABC), линия наибольшего ската k (k Î ∆ ABC, k ₁ ┴ h₁).

Поверхности

В математике поверхность рассматривается как непрерывное множество точек пространства, координаты которых удовлетворяют уравнению: F(x, y, z) =0.

Так как в НГ геометрические фигуры задаются графически, поэтому способ образования поверхностей в НГ – кинематический: поверхность представляется как совокупность всех последовательных положений некоторой линии, перемещающейся в пространстве по определенному закону.

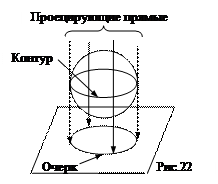Линию, производящую поверхность, называют образующей. При своем движении образующая может пересекать одну или несколько неподвижных линий – направляющих.

Способы задания поверхности на чертеже

1. Определителем – совокупность независимых условий, однозначно определяющих поверхность (геометрические фигуры с помощью которых может быть задана поверхность, закон образования ).

2. Очерком – проекцией видимого контура поверхности на плоскость проекций (рис.22).

В зависимости от вида образующей поверхности делятся на:

1) линейчатые (образующая - прямая);

1.1) развертывающиеся – можно без складок и разрывов совместить с плоскостью, основной признак – наличие ребра возврата S, т.е. пространственной кривой, касательно к которой располагается образующая a во всех положениях своего перемещения по направляющей m.

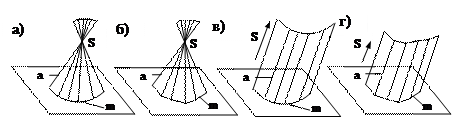Примеры (рис.20):

а) коническая (ребро возврата – собственная точка S), б) пирамида (направляющая m –ломаная линия),

в) цилиндрическая (точка S удалена в бесконечность),

г) призма (направляющая m –ломаная линия);

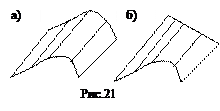
1.2) неразвертывающиеся (рис.21) – а) цилиндроид (2 направляющие – кривые), б) коноид (1 направляющая – кривые, 2-я - прямая).

2) нелинейчатые (образующая - кривая) – тор, сфера.

Свойство принадлежности точки поверхности:

точка принадлежит поверхности если она лежит на линии, принадлежащей этой поверхности, в качестве вспомогательных линий следует выбирать прямые, окружности (напр. для линейчатых поверхностей целесообразно выбирать прямолинейные образующие).

В зависимости от закона движения образующей поверхности делятся на:

1) вращения (поверхность образована вращением образующей) – тор, сфера, цилиндр, конус, поверхности второго порядка – эллипсоид, параболоид, гиперболоид ;

2) параллельного переноса (поступательное движение образующей);

3) винтовые (винтовое движение образующей) - геликоид.

В зависимости от вида направляющей поверхности делятся на:

1) кривыми (направляющая – кривая линия) - цилиндроид;

2) гранными (направляющая – ломаная линия) – пирамида, призма.

Одну и ту же поверхность можно образовать различными способами, выбирать следует наиболее простой в исполнении и удобный для решения задач (пример - конус).

Лекция № 2

Поверхности вращения

Поверхностью вращения называется поверхность, образованная вращением криволинейной или прямолинейной образующей вокруг неподвижной прямой - оси поверхности (рис.23 ).

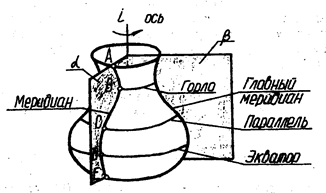
Рис.23

Каждая точка при своем образующей при своем движении вокруг оси описывает окружность, которая называется параллелью. Плоскости этих окружностей распложены перпендикулярно оси. Параллель наибольшего радиуса называется ЭКВАТОРОМ, наименьшего радиуса - ГОРЛОМ поверхности.

Плоскости проходящие через ось вращения. Называются меридиальными плоскостями (плоскости а и b на рис. 23). Линии поверхности. принадлежащие этим плоскостям, называются меридианами.

Меридиан. расположенный параллельно плоскости проекций, называется главным меридианом. Он проецируется без искажения на эту плоскость проекций.

Рис.24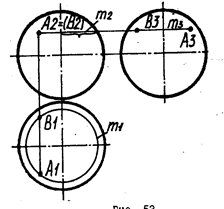

Для построения недостающих проекций точек, принадлежащих поверхностям вращения. в качестве вспомогательных линий целесообразно использовать окружности - параллели поверхностей. На рис. 24 показано построение проекций точек А и В с помощью параллелей поверхности сферы. Проекции невидимых точек заключены в круглые скобки.