Частные виды поверхностей вращения

СФЕРА образуется вращением окружности вокруг своего диаметра (рис.25).

ЦИЛИНДР образуется вращением прямолинейной образующей а вокруг оси 1 (рис. 26).

КОНУС образуется вращением прямолинейной образующей а, пересекающей ось 1, вокруг оси 1 (рис.26).

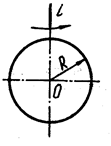
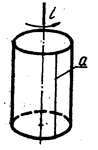
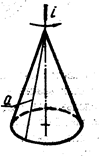
Рис. 25 Рис.26 Рис.27

При вращении кривых второго порядка: эллипса, параболы. гиперболы образующая поверхности вращения второго порядка: эллипсоид, параболоид, гиперболоид.

П О 3 И Ц И О Н Н Ы Е 3 А Д А Ч И

Рассмотрим 2 типа позиционных задач:

- задачи на принадлежность (рассмотрены выше)

- задачи на пересечение геометрических фигур.

Рассмотрим решение задач на пересечение поверхностей проецирующей плоскостью и взаимное пересечение поверхностей, одна из которых занимает проецирующее положение.

СЕЧЕНИЯ ПОВЕРХНОСТЕЙ

При пересечении поверхности плоскостью получается плоская фигура, которая называется сечением.

Плоское сечение кривой поверхности в общем случае представляет собой плоскую кривую. которая в частном случае может выродиться в одну или две прямые.

Построение плоского сечения следует начинать с анализа заданных геометрических образов (поверхности и плоскости) и определения вида искомой плоской кривой (окружность, гипербола, эллипс и т. д.).

Кривая линия может быть построена или по принадлежащим ей точкам, или по известным параметрам, например, радиус окружности. большая и малая оси эллипса и т.д.

Построение проекций линии сечения следует начинать с определения опорных точек, то есть точек, определяющих границы, характер и видимость кривой по отношению к плоскостям проекций.

К числу опорных точек относятся:

1) высшая и низшая - точки наиболее и наименее удаленные от той или иной плоскости проекций;

2) видимости - точки, разделяющие кривую на видимый и невидимый участки (они расположены на очерковых линиях поверхности);

3) наибольшей и наименьшей ширины кривой;

4) характерные. точки кривой. К ним относятся точки перегиба, излома и другие точки.

После определения опорных точек находят промежуточные точки. Число их должно быть достаточным для построения проекций сечения.

СЕЧЕНИЯ МНОГОГРАННИКОВ

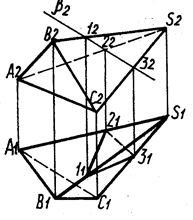
Рис.28

Плоское сечение многогранника имеет вид многоугольника, который можно построить. двумя способами:

Способом ребер, определяя точки пересечения ребер многогранника с секущей плоскостью. то есть многократно решая задачу на пересечение прямой с плоскостью. или

Способом граней, строя линии пересечения граней многогранника с плоскостью, то есть многократно решая задачу на пересечение двух плоскостей.

Выбор способа должен обеспечить рациональное решение задачи. На рис. показано построение сечения пирамиды фронтально - проецирующей плоскостью(рис.28).

Так как секущая плоскость проецирующая, то сначала определяется фронтальная проекция 1₂ 2₂ 3₂ сечения. Она совпадает с фронтальной проекцией b₂ плоскости b (в силу собирательного свойства этой проекции плоскости).

Горизонтальная проекция строится по точкам, исходя из условия принадлежности точек сечения ребрам пирамиды (способ ребер): 1ÎSB, 2 Î SA, ЗÎ SC.

Горизонтальная проекция линии сечения 1,2,3, проводится с учетом видимости граней пирамиды.

ЧАСТНЫЕ ВИДЫ ПЛОСКИХ СЕЧЕНИЙ

(цилиндрические; конические, сферические)

При пересечении частных видов поверхностей вращения плоскостью получаются заранее известные кривые (окружность. парабола, гипербола и др.). которые могут быть построены по основным параметрам,

определяющим эту кривую (например, радиус окружности, большая и малая оси эллипса и др.).

ЦИЛИНДРИЧЕСКИЕ СЕЧЕНИЯ

При пересечении цилиндра вращения плоскостью могут быть получены линии, наглядные изображения которых даны на рис. - .

Изображения проекций линий плоских сечений цилиндра приведены на рис. 32.

Окружность получается, если секущая плоскость а перпендикулярна оси цилиндра (рис.29). Диаметр окружности d равен диаметру цилиндра (рис.32).

Эллипс- если секущая плоскость р не параллельна ни одной образующей цилиндра (рис.30). Большая ось АВ эллипса равна отрезку А₂В₂ , малая ось CD равна диаметру d цилиндра (рис.32).

Две прямые (образующие) - если секущая плоскость параллельна оси цилиндра (рис.31). На рис.32 это образующие, проходящие. через точки 1 и 2.

Так как цилиндр является горизонтально - проецирующим и каждая из секущих плоскостей тоже занимает проецирующее положение, то построение проекций линий пересечения не требуется: они находятся на чертеже без дополнительных построений: либо совпадают с проекциями плоскости (a₂ b₂), либо цилиндра (с окружностью горизонтального очерка цилиндра).

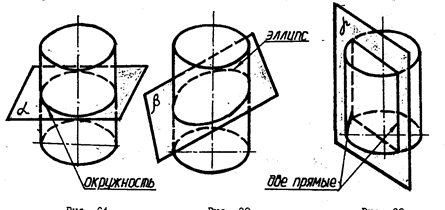
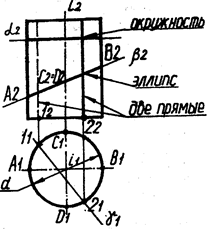
Рис.29 Рис.30 Рис.31 Рис.32

КОНИЧЕСКИЕ СЕЧЕНИЯ

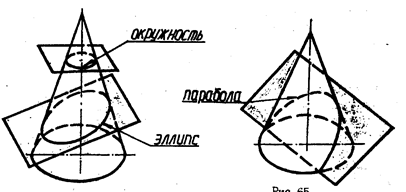
Рис. 33

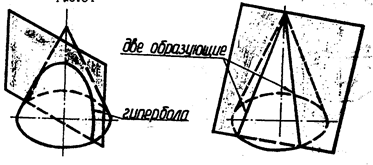
Рис. 34

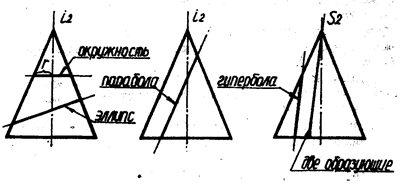
Рис.35 Рис. 36 Рис.37

При пересечении конуса вращения плоскостью могут быть получены кривые второго порядка: окружность, эллипс, парабола и гипербола или в частном случае две прямые - образующие конуса. Наглядные изображения конических сечений приведены на рис. 33 - 37.

Окружность получается. если секущая плоскость перпендикулярна оси конуса (рис. 33). Радиус окружности r равен расстоянию от оси конуса до его очерковой образующей (рис.35).

Эллипс - если секущая плоскость не параллельна ни одной из образующих конуса (рис. 33 и 35).

Парабола - секущая плоскость параллельна одной образующей конуса (рис. 33 и 36).

Две образующих- секущая плоскость проходит через вершину конуса (рис.34 и рис. 37).

Гипербола - секущая плоскость параллельна двум образующим конуса (в частном случае параллельна его оси) (рис. 34 и 37).

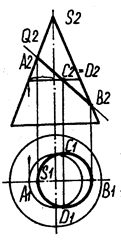
Рис. 38

На рис. 38 дано построение проекций сечения конуса плоскостью а, заданная плоскость - фронтально - проецирующая. Она не параллельна ни одной из образующих конуса, поэтому в сечении получается эллипс. Построение эллипса возможно. если известны размеры его осей.

Большая ось АВ эллипса проецируется на фронтальную плоскость без искажения и равна отрезку А₂В₂,. Малая ось CD эллипса проецируется на фронтальную плоскость проекций в точку С₂ = Р₂ ). расположенную в середине отрезка А₂В_{2 .} Величина малой оси CD определяется на горизонтальной проекции из условия принадлежности точек С и D поверхности конуса и равна отрезку С, D,. .Для построения точек С₁ и D₁ через точки С и D на поверхности конуса проводится вспомогательная окружность. на горизонтальной проекции которой находятся точки С₁ и D_1.

СФЕРИЧЕСКИЕ СЕЧЕНИЯ

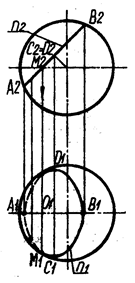
Рис. 39

Сечение сферы любой плоскостью представляет собой окружность. Проекции линий сечения сферы показаны на рис. 24 и 39.

Окружность сечения может проецироваться в виде:

- отрезка прямой, если секущая плоскость перпендикулярна плоскости проекций (отрезок А₂В₂,):

- окружности, если секущая плоскость параллельна плоскости проекций (проекция m₁ на рис. 72). Величина диаметра d окружности сечения определяется 6трезком А₂В₂ проекции секущей плоскости, расположенным внутри очерка сферы. Проекция центра окружности О₂ находится на середине этого
отрезка.

- эллипса, если секущая плоскость наклонна к плоскости проекций.

Лекция № 3