Применение преобразования Лапласа к решению дифференциальных уравнений
Необходимость определения постоянных интегрирования из начальных условий в ряде случаев значительно усложняет расчет переходных процессов классическим методом решения линейных дифференциальных уравнений, описывающих исследуемые процессы. По мере усложнения электрических схем и возрастания порядка дифференциальных уравнений трудности, связанные с нахождением постоянных интегрирования, возрастают.
Для инженерной практики более удобным является метод решения линейных дифференциальных уравнений, при котором заданные начальные условия включаются в исходные уравнения и для нахождения искомой функции не требуется дополнительного определения постоянных интегрирования.
Идея этого метода заключается в том, что из области функции действительного переменного 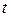 решение переносится в область функции комплексного переменного
решение переносится в область функции комплексного переменного 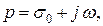 где операции принимают более простой вид. А именно: вместо исходных дифференциальных или интегро-дифференциальных уравнений получаются алгебраические уравнения, затем, производится обратный переход в область функций действительного переменного.
где операции принимают более простой вид. А именно: вместо исходных дифференциальных или интегро-дифференциальных уравнений получаются алгебраические уравнения, затем, производится обратный переход в область функций действительного переменного.
Взаимное соответствие между функцией времени (оригиналом)  и ее изображением
и ее изображением 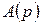 в операторном методе устанавливается с помощью прямого
в операторном методе устанавливается с помощью прямого
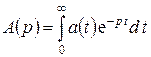 и обратного
и обратного 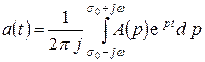 преобразований Лапласа и указывается знаком соответствия:
преобразований Лапласа и указывается знаком соответствия: 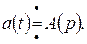
Функция 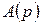 называется операторным изображением функции
называется операторным изображением функции  или изображением функции
или изображением функции  по Лапласу. Исходная функция времени по отношению к своему операторному изображению является оригиналом. Комплексное число p будем называть оператором преобразования Лапласа или комплексной частотой.
по Лапласу. Исходная функция времени по отношению к своему операторному изображению является оригиналом. Комплексное число p будем называть оператором преобразования Лапласа или комплексной частотой.
Некоторые свойства преобразования Лапласа.
1. Изображение по Лапласу постоянной величины K равно этой величине, деленной на p:
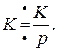
2. Умножение функции времени  на постоянное число K соответствует умножение на это же число ее изображения:
на постоянное число K соответствует умножение на это же число ее изображения:
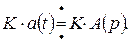
3. Изображение суммы функций времени равно сумме изображений этих функций:
 где
где 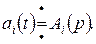
4. Если начальное значение функции  равно нулю:
равно нулю: 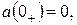 то дифференцированию функции
то дифференцированию функции  соответствует умножение изображения этой функции на p (теорема дифференцирования):
соответствует умножение изображения этой функции на p (теорема дифференцирования):

При 

5. Интегрированию функции времени в пределах от 0 до t соответствует деление изображения этой функции на p (теорема интегрирования):

6. Смещению функции времени на t0 соответствует деление изображения этой функции на p (теорема запаздывания):

7. Смещению изображения 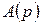 на комплексной плоскости на комплексное число
на комплексной плоскости на комплексное число 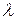 соответствует умножение оригинала на
соответствует умножение оригинала на 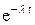 (теорема смещения):
(теорема смещения): 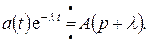
8. Умножению аргумента оригинала на постоянное число 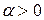 соответствует деление аргумента изображения и самого изображения на это же число (теорема изменения масштаба, теорема подобия):
соответствует деление аргумента изображения и самого изображения на это же число (теорема изменения масштаба, теорема подобия):
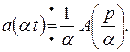
9. Если изображение 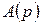 может быть представлено в виде отношения двух полиномов от p, не имеющих общих корней
может быть представлено в виде отношения двух полиномов от p, не имеющих общих корней

причем степень полинома  выше, чем степень полинома
выше, чем степень полинома  , а уравнение
, а уравнение 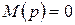 не имеет кратных корней, то для перехода от изображения к оригиналу можно воспользоваться теоремой разложения:
не имеет кратных корней, то для перехода от изображения к оригиналу можно воспользоваться теоремой разложения:
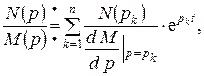
где 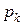 —корни уравнения
—корни уравнения 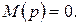
Если в уравнении 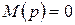 один корень равен нулю, то полином
один корень равен нулю, то полином  можно представить в виде
можно представить в виде 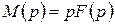 , а оригинал находят по формуле
, а оригинал находят по формуле
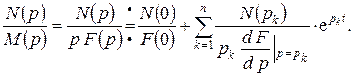 (3.2)
(3.2)
Если среди m корней уравнения 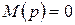 имеется n — вещественных и
имеется n — вещественных и  — комплексных, то обозначив вещественные корни через
— комплексных, то обозначив вещественные корни через 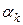 (k=1, 2, … , n), а комплексные — через
(k=1, 2, … , n), а комплексные — через 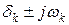
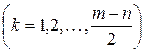 и положив
и положив

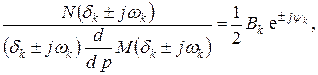
тогда
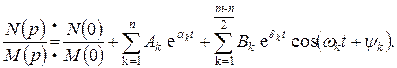 (3.3)
(3.3)
Теорема разложения в сочетании с другими свойствами преобразования Лапласа дает возможность составить таблицы оригиналов и изображений, значительно облегчающие и ускоряющие расчеты переходных процессов. Следует отметить, что в ряде справочников приведены таблицы преобразований Лапласа–Карсона  которое отличается от преобразования Лапласа только наличием множителя p.
которое отличается от преобразования Лапласа только наличием множителя p.
Дата добавления: 2020-10-14; просмотров: 673;











