Включение rL цепи на постоянное напряжение

Пусть дана цепь (рис.6.1), которая подключается к источнику постоянного напряжения. Параметры цепы заданы: r, L, 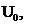ключ K работает на замыкание.

Определить ток i (t).

Решение:

В последний момент времени перед замыканием ключа ток в цепи отсутствовал

i(0-) = 0,

где t = 0-.

При t = 0₊ ключ замыкается. Здесь t = 0₊ – первый момент времени после совершения события (замыкания ключа).

Рис. 6.1

Ключ замкнулся, образовался контур. Составим для него уравнение второго закона Кирхгофа:

.

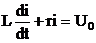Это уравнение аналогично математическому дифференциальному уравнению первого порядка (ax’ + bx = y).

Решение для тока имеет вид:

,

где 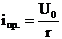– принужденная составляющая решения, А – постоянная интегрирования, которая может быть найдена из граничных условий.

По характеристическому уравнению: Lp + r = 0, где p=d/dt

определим корень: .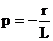

Обратная величина модуля корня называется постоянной переходного процесса, определяет время переходного процесса:

,

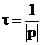а время переходного процесса равно: t_п.п = (4…5) τ.

В момент времени 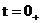определим постоянную интегрирования А.

Подставим в решение для тока этот момент:

.

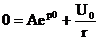Отсюда А равно:

.

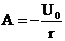Окончательное решение для тока:

.

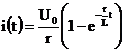Законы коммутации

Законы коммутации дает возможность определить постоянные интегрирования, так как для их нахождения требуется точно знать значения токов (напряжений), а иногда их производных при t=0.