Расчет переходных процессов в цепях с синусоидальными источниками классическим методом

<25 26 272829 30 31 >

Пусть для цепи (рис. 6.13) дано: .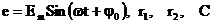

Определить:

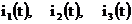
Начальные условия при :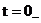

;

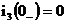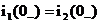Определим эти токи комплексным Рис.6.13 методом по схеме замещения (рис. 6.14):

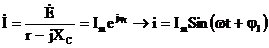Тогда при 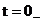токи равны:

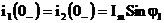Напряжение на конденсаторе:

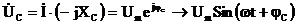При t = 0_-

По закону коммутации:

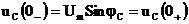При t = 0₊составим схему замещения (рис. 6.15), где .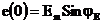

Рис. 6.14

Составим уравнения процессов в цепи по законам Кирхгофа:

После решения этих уравнений получим:

; ; .

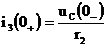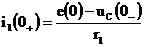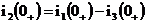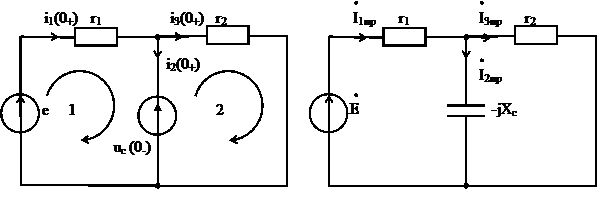
Рис. 6.15 Рис. 6.16

При t >>0 определим принужденные составляющие: .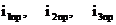

Для этого составим схему замещения (рис. 6.16). Комплексным методом определим токи и переведем их во временную область:

;

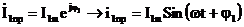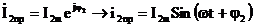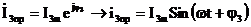Находим корень характеристического уравнения. Для этого оьносительно источника находим входное сопротивление.

После преобразований получаем

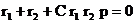тогда корень характеристического уравнения равен: .

Решение для первого тока:

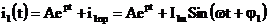Постоянную интегрирования А найдем при :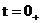

;

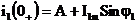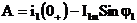Решение для второго тока аналогично:

;

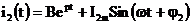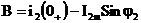Третий ток найдем по первому закону Кирхгофа:

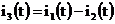6.1.5.Порядок анализа переходных процессов классическим методом

В общем случае расчет переходных процессов классическим методом осуществляется в следующем порядке.

1. Анализ цепи до коммутации В результате этого анализа определяют токи в индуктивностях и напряжения на емкостях в момент времени, непосредственно предшествующий коммутации ( ).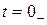

2. Определение независимых начальных условий. Независимые начальные условия представл Ияют собой токи в индуктивностях и напряжения на емкостях в момент времени 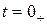. Независимые начальные условия находятся с помощью законов коммутации или принципов непрерывности потокосцепления и электрического заряда.

3. Анализ установившегося процесса в цепи после коммутации. В результате анализа установившегося процесса в цепи после коммутации находится принужденная составляющая реакции цепи (частное решение дифференциального уравнения цепи).

4. Определение свободной составляющей реакции цепи. На этом этапе составляе тся характеристическое уравнение цепи. Находятся его корни, и определяется общий вид свободной составляющей реакции цепи (общее решение линейного однородного дифференциального уравнения, соответствующего дифференциальному уравнению цепи после коммутации).

5. Нахождение общего вида реакции цепи. Находится путем суммирования свободной и принужденной составляющих цепи.

6. Определение постоянных интегрирования. Постоянные интегрирования находятся по зависимым начальным условиям.

7. Окончательная запись реакции цепи.

<25 26 272829 30 31 >

Дата добавления: 2020-10-14; просмотров: 447;