Уточнение корней до заданной точности.
То есть сужение отрезка локализации корня [a,b]. Рассмотрим несколько методов.
Метод половинного деления (дихотомии).
Пусть корень отделён и принадлежит отрезку 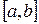 . Находим середину отрезка
. Находим середину отрезка 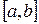 по формуле
по формуле 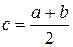 (рис.3). Если
(рис.3). Если 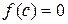 , то с – искомый корень.
, то с – искомый корень.
|
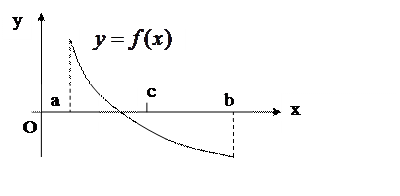
Рис. 3.
Рис.3
Вычисляем 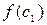 , выбираем отрезок
, выбираем отрезок 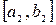 и т.д. Как только будет выполнено
и т.д. Как только будет выполнено 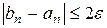 , то в качестве приближенного значения корня, вычисленного с точностью
, то в качестве приближенного значения корня, вычисленного с точностью 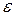 , можно взять
, можно взять 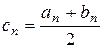 . После каждой итерации отрезок, на котором расположен корень уменьшается вдвое, то есть после n итераций он сокращается в 2n раз. Таким образом, число итераций n в данном методе зависит от предварительно заданной точности ε и от длины исходного отрезка и не зависит от вида функции f(x). Это является важным преимуществом метода половинного деления по сравнению с другими методами. Метод, однако, медленно сходится при задании высокой точности расчёта.
. После каждой итерации отрезок, на котором расположен корень уменьшается вдвое, то есть после n итераций он сокращается в 2n раз. Таким образом, число итераций n в данном методе зависит от предварительно заданной точности ε и от длины исходного отрезка и не зависит от вида функции f(x). Это является важным преимуществом метода половинного деления по сравнению с другими методами. Метод, однако, медленно сходится при задании высокой точности расчёта.
Метод хорд.
Пусть на отрезке [a,b] функция f(x) непрерывна и принимает на концах отрезка значения разных знаков, а производные f ′(x) и f ″(x) сохраняют постоянный знак на интервале (a,b). Тогда возможны четыре случая расположения дуги кривой (рис.4).
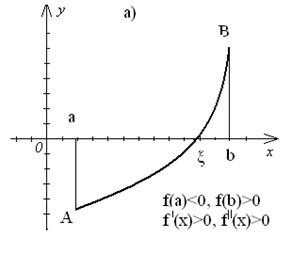
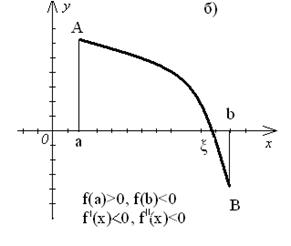
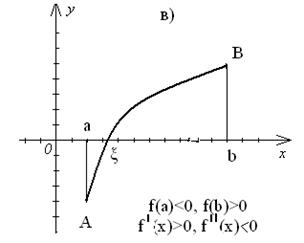
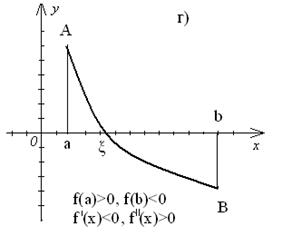
Рис.4.
В методе хорд за очередное приближение берём точку пересечения с осью Х прямой (рис.5), соединяющей точки (a,f(a)) и (b,f(b))
Причём одна из этих точек фиксируется − та, для которой знаки f(x) и f ″(x) одинаковы.
Для рис.5 неподвижным концом хорды является х =a.
Уравнение хорды АВ: 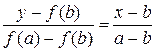
Точка пересечения хорды с осью Х (у=0): 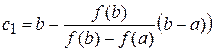 .
.
Теперь корень находится на отрезке [a,c1]. Заменяем b на с1.
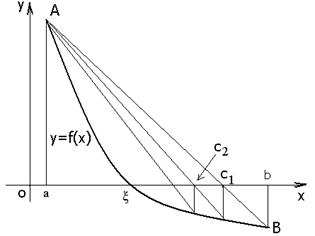
Рис.5. Иллюстрация метода хорд.
Применяя метод хорд к этому отрезку, получим:
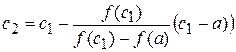 .
.
Продолжим и т.д., получим: 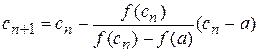 (2)
(2)
Условие окончания вычислений:
│сn+1 − cn│< ε или │f(cn)│< ε1.
Для оценки погрешности можно пользоваться общей формулой:
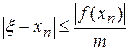 , где
, где 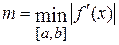
Итак, если f (x)∙f″(x) > 0, то приближённое значение корня находят по формуле (2), если f′(x)∙f″(x) < 0 (т.е. фиксируется х = b), то по формуле:
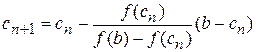 . (3)
. (3)
Дата добавления: 2020-10-14; просмотров: 645;

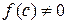 , то в качестве нового отрезка изоляции корня
, то в качестве нового отрезка изоляции корня 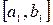 выбираем ту половину
выбираем ту половину 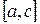 или
или 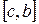 , на концах которой
, на концах которой 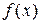 принимает значения разных знаков. Другими словами, если
принимает значения разных знаков. Другими словами, если 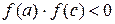 , то корень принадлежит отрезку
, то корень принадлежит отрезку 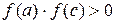 - отрезку
- отрезку 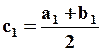 ,
,










