Напряжение. Напряженное состояние в точке тела

Нагруженное тело мысленно рассечем плоскостью, и действие отброшенной части заменим действием внутренних сил. В сечении выберем произвольную точку, а в её окрестности элементарную площадку DF. Равнодействующую сил, действующих на площадку, обозначим DР (рис.16).

Рис.16

Среднее полное напряжение на заданной площадке будет равно:

Р_ср = .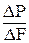

Если площадку уменьшать, то в пределе она обратится в точку. Напряжение -это предел отношения внутренней силы к площади, на которой она действует при условии, что площадь стремится к нулю. Р – полное напряжение [Н/м²].

P = lim_DF®0 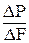. (16)

Вектор полного напряжения можно разложить на проекции (рис.17). Проекцию полного напряжения на нормаль к плоскости сечения будем называть нормальным напряжением (обозначаетсяs), а проекцию полного напряжения на плоскость сечения – касательным напряжением (обозначается t). Вектор нормали к сечению обозначим через n.

Р = 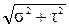(17)

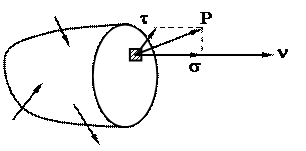Рис.17

Направление касательного напряжения не однозначно, что создает неудобство при математической обработке, поэтому его раскладывают по координатным осям в плоскости сечения. Возьмем правую систему координат. Тело рассечем перпендикулярно оси Z (рис.18).

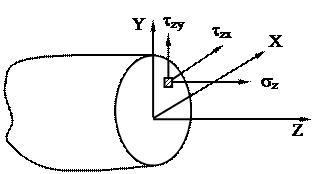Рис.18

=

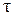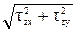
Индекс нормального напряжения соответствует оси, перпендикулярной плоскости сечения. Индексы касательного напряжения проставляются следующим образом: первый индекс соответствует оси, перпендикулярной плоскости сечения, в котором лежит касательное напряжение, второй индекс соответствует оси, которой параллельно касательное напряжение.

Проводя другие плоскости, будем получать другие значения напряжений. Совокупность напряжений по всем плоскостям, проходящим через заданную точку, называется напряженным состоянием в точке тела.

В общем случае в точке твердого деформированного тела может возникнуть 9 напряжений: 3 нормальных и 6 касательных. Эти напряжения образуют тензор напряжений:

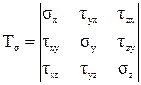(18)