Метод сечений. Внутренние силы

Для изучения внутренних явлений в теле используется метод сечений.

Рис.13

Все тело находится в равновесии. После мысленного разрезания и отбрасывания правой части её действие должно быть заменено системой сил (рис.13) в сечении, сохраняющих равновесие левой части. Такие же силы, но противоположного направления действуют на правую часть.

Для удобства приводим все силы, действующие в сечении, к центру тяжести; в результате этого получается главный вектор сил и главный вектор моментов (рис.14).

Рис.14

Разложим главные вектора по осям в правой системе координат: Q (Q_x, Q_y, Q_z); M (M_x, M_y, M_z) (рис.15).

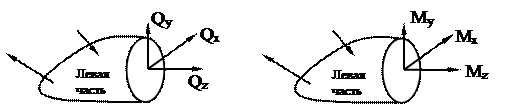Рис.15

Проекции имеют определенные названия: Q_x, Q_y – поперечные силы; Q_z – продольная сила; M_x, M_y – изгибающие моменты; M_z – крутящий момент.

Сила считается положительной, если ее направление совпадает с осью, момент считается положительным, если он создает вращение против часовой стрелки (смотреть необходимо с конца соответствующей оси). Эти шесть проекций называют интегральными характеристиками напряжений.

Всё тело до рассечения находилось в равновесии. Так как силы, действующие в сечении, заменяют действие отброшенной части, то и оставшаяся часть должна находится в равновесии, следовательно, к ней применимы уравнения статики.

SХ=0,

Р_1х + Р_2х + …+ Q_х = 0,

Q_х = - (Р_1х + Р_2х + …).

Проекция главного вектора внутренних сил на ось Х равна сумме проекций на эту ось всех внешних сил, действующих на левую часть, взятых с противоположными знаками. Аналогично получаем выражения для остальных проекций главного вектора внутренних сил и главного вектора момента внутренних сил.

Q_у = - (Р_1у + Р_2у + …),

Q_z = - (Р_1z + Р_2z + …),

M_х = - (M_хp1 + M_хp2 + …), (15)

M_у = - (M_уp1 + M_уp2 + …),

M_z = - (M_zp1 + M_zp2 + …).

Полученные уравнения дают лишь интегральные характеристики внутренних сил, но не дают информации о распределении сил по сечению.