Нормальные напряжения в плоскости поперечного сечения

Определим величину нормального напряжения в плоскости поперечного сечения, зная интегральные характеристики в этом сечении. Предположим, что нормальные напряжения в сечении распределены по линейному закону:

s(х,у) = а + b×х + с×у (24)

С нормальным напряжением в сечении связаны продольная сила и два изгибающих момента. Подставим в выражения (19), (21) и (22) наше предположение о линейной зависимости напряжения от координат в сечении (24):

N = = =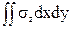

= + + =

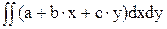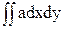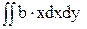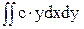= а×F+b×S_y+c×S_x

M_x = = =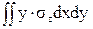

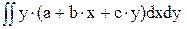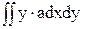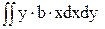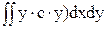= + + = a×S_x+b×I_xy+c×I_x (25)

M_у = - = - =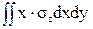

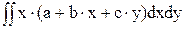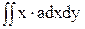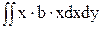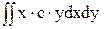= - - - = -a×S_y-b×I_y-c×I_xy

Выражения (25) были получены для произвольного положения осей. Их можно упростить, взяв в качестве системы координат главные центральные оси. По определению в этих осях статические и центробежный моменты инерции равны нулю (S_x= S_у= 0, I_xy=0).

N = а×F

M_x = c×I_x (26)

M_у = -b×I_y

Из полученных выражений можно найти коэффициенты а, b и с:

а = N/F, с = M_x /I_x , b = -M_у /I_y (27)

Подставив полученные значения коэффициентов в наше предположение о распределении нормального напряжения по сечению (24), получим

s = 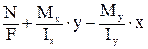, (28)

где N – продольная сила в сечении; М_х, М_у – изгибающие моменты в сечении; F – площадь поперечного сечения; I_х, I_у – главные осевые моменты инерции сечения; х, у – координаты точки, в которой вычисляется напряжение относительно главных центральных осей.