Закон парности касательных напряжений

В окрестностях произвольной точки напряженного тела выделим элементарный объём в форме прямоугольного параллепипеда со сторонами dx, dy, dz. На каждой из граней действует по три составляющих напряжения: нормальное напряжение и два касательных (рис.20).

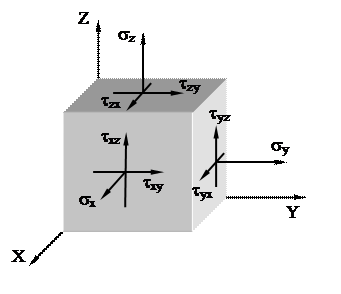Рис.20

Составим уравнение равновесия выделенного элемента в форме суммы моментов всех сил относительно оси X:

SМ_х = 0,

s_у×dx×dz×dy - s_у×dx×dz×dy + s_z×dx×dy×dz - s_z×dx×dy×dz + t_xy×dy×dz× 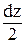- t_xy×dy×dz× +

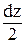+ t_xz×dy×dz× 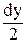- t_xz×dy×dz× 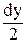+ t_zy×dx×dy×dz - t_yz×dx×dz×dy = 0,

приведя подобные слагаемые и упростив выражение, получим:

t_zy = t_yz. (29)

Составляя уравнения равновесия относительно осей Y и Z, получим аналогичные выражения:

t_zх = t_хz, (30)

t_хy = t_yх.

Полученные выражения (29), (30) определяют закон парности касательных напряжений: касательные напряжения на взаимно перпендикулярных площадках равны по величине и направлены либо к общему ребру, либо от него.