Изменение геометрических характеристик при повороте координатных осей

Рис.11

Пусть известны геометрические характеристики сечения относительно осей ХY. Требуется определить геометрические характеристики сечения относительно осей Х₁Y₁. Известно, что оси этих двух систем координат повернуты друг относительно друга на угол a и имеют общее начало координат (рис.11). Координаты любой точки в новой системе координат можно выразить через координаты в прежней системе координат:

х₁=х×cosa+y×sina, (12)

у₁=у×cosa-x×sina.

Запишем геометрические характеристики в новой системе координат по определению и сделаем замену «новых» координат на предыдущие:

I_х1= = =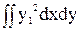

= =

= - + =

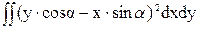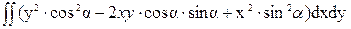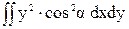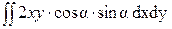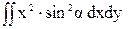= I_х×cos²a - I_ху×sin2a + I_у×sin²a ; (13)

I_у1= = =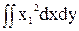

= =

= + + =

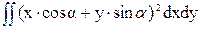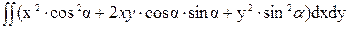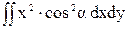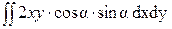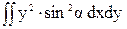= I_y×cos²a + I_ху×sin2a + I_x×sin²a ;

I_х1у1= = =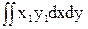

= =

= - + -

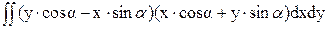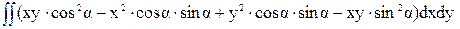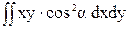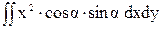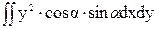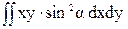- = I_ху×cos²a - 0,5×I_y×sin2a +0,5×I_x×sin2a - I_ху×sin²a =

= I_ху×cos2a - 0,5×sin2a×(I_y - I_x) .

Необходимо помнить, что угол a, входящий в формулы, необходимо подставлять с учетом знака.

Сложим выражения для осевых моментов инерции при повороте координатных осей.

I_х1 + I_у1 = I_х×(cos²a + sin²a) + I_у×(sin²a + cos²a ) + I_ху×(sin2a- sin2a) = I_х + I_у.

Отсюда можно сделать вывод, что при повороте координатных осей сумма осевых моментов инерции неизменна и равна полярному моменту инерции относительно начала координат.

Рассмотрим частный случай. Пусть оси Х₁Y₁ – главные центральные, тогда

I_х1у1= I_ху×cos2a - 0,5×sin2a×(I_y – I_x) = 0,

tg2a = 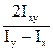. (14)

Необходимо помнить, что при решении задач угол, рассчитанный по формуле (14), откладывается против часовой стрелки, если он положителен и по часовой стрелке, если отрицателен.