Геометрические характеристики сложных сечений

При вычислении геометрических характеристик сложных сечений последние обычно разбивают на отдельные простые части, геометрические характеристики которых известны (для простых фигур они приведены в справочниках). Из основного свойства интеграла суммы следует, что геометрические характеристики сложной фигуры равны сумме геометрических характеристик её составных частей. Заметим, что в случае, когда в сечении имеется отверстие, его геометрические характеристики необходимо вычитать. Также следует учесть, что суммирование или вычитание геометрических характеристик можно производить только в том случае, если они посчитаны относительно одних и тех же осей. Поэтому, если оси простых фигур не совпадают, предварительно необходимо, используя формулы параллельного переноса (10), пересчитать геометрические характеристики относительно одной и той же оси.

Пример. Определить положение главных центральных осей и значения геометрических характеристик относительно них для сложного сечения представленного на рис.12.

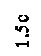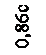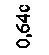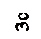Рис.12

Разобьем данное сечение на элементарные фигуры, геометрические характеристики которых известны по справочникам. Оси Х₁У₁ – центральные оси первой фигуры. Оси Х₂У₂ – центральные оси второй фигуры.

1 фигура - треугольник:

F₁=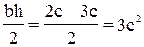

S_x1=0

S_y1=0

I_x1=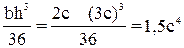

I_y1=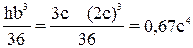

I_x1y1=-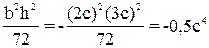

2 фигура - прямоугольник:

F₂ = bh = 4c∙c = 4c²

S_x2=0

S_y2=0

I_x2=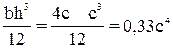

I_y2=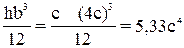

I_x2y2=0

Заметим, что центробежный момент инерции прямоугольника равен нулю, т. к. фигура имеет ось симметрии.

За вспомогательные оси, относительно которых вычисляем координаты центра тяжести всего сечения, принимаем Х₁У₁.

Х_с= =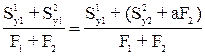

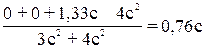
У_с= 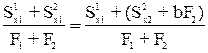= 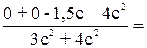- 0,86c

По полученным значениям координат центра тяжести находим положение центральных осей всего сечения.

Найдем геометрические характеристики всего сечения относительно центральных осей. Так как оси параллельны, воспользуемся формулами преобразования при параллельном переносе осей.

S_xс=0

S_yс=0

I_xc =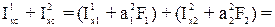

=(1,5с⁴ + (0,86с)²∙3с²) + (0,33с⁴ + (-0,64с)²∙4с²) = 5,69с⁴

I_yc =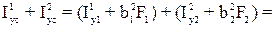

=(0,67с⁴ + (-0,76с)²∙3с²) + (5,33с⁴ + (0,57с)²∙4с²) = 9,03с⁴

I_xcyc =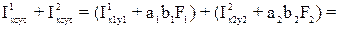

=(-0,5с⁴ + (0,86с)∙(-0,76с)∙3с²) + (0 + (-0,64с)∙(0,57с)∙4с²) = -3,92с⁴

Найдем положение главных центральных осей сечения. Для этого определяем угол поворота центральных осей.

tg2a= 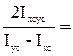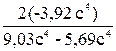= – 2,35,

a=0,5arctg(- 2,35) = - 33,5°.

Так как получили отрицательный угол, то поворачиваем центральные оси по часовой стрелке.

Найдем значения геометрических характеристик относительно главных центральных осей сечения Х₀У₀:

I_х0= I_хc×cos²a - I_хcуc×sin2a + I_уc×sin²a = 5,69с⁴ ∙cos²(-33,5) + 3,59c⁴∙sin(-67) + 9,03с⁴∙sin²(- 33,5) = 3,4с⁴ ;

I_у0= I_yc×cos²a + I_хcуc×sin2a + I_xc×sin²a = 9,03с⁴∙ cos²(-33,5) – 3,59c⁴∙sin(-67) + 5,69с⁴∙ sin²(- 33,5) = 11,32с⁴;

I_х0у0= I_хcуc×cos2a - 0,5×sin2a×(I_yc - I_xc) = - 3,92× cos(-67) – 0,5×sin(-67)×(9,03с⁴ – 5,69с⁴) = 0.

Статические моменты инерции сечения при повороте осей проходящих через центр тяжести не меняются и остаются равными нулю.