Интегральные характеристики напряжений в точке

Установим связь между интегральными характеристиками напряжений и напряжениями в сечении.

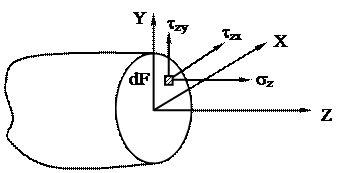Рис.19

Выберем бесконечно малую площадку dF = dxdy. На этой площадке действуют нормальное напряжение s_z и касательные напряжения t_zx, t_zy (рис.19). Для того, чтобы найти элементарную продольную силу, необходимо умножить нормальное напряжение на площадь площадки, на которой оно действует (t_zx, t_zy перпендикулярны оси Z и поэтому не входят в состав продольной силы). Так как таких элементарных площадок по сечению бесконечно много, то, чтобы найти полную продольную силу, необходимо проинтегрировать элементарную продольную силу по площади поперечного сечения:

dN=s_z×dxdy,

N= 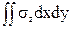. (19)

Аналогично поступаем для получения выражений поперечных сил:

Q_x= ,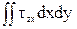

Q_y= 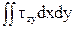. (20)

Для получения выражений изгибающих и крутящего моментов напомним, что момент - это произведение силы на плечо (плечо - это кратчайшее расстояние от оси до линии действия силы). Вокруг оси Х момент создает только сила s_z×dxdy (сила t_zх×dxdy не создает момент, так как параллельна оси Х; сила t_zу×dxdy не создает момент, так как пересекает ось), плечом для этой силы является координата Y точки действия силы. Момент положительный, так как создает вращение против часовой стрелки:

M_x = 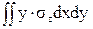. (21)

Аналогично поступаем для получения выражений моментов M_у и M_z:

M_у =- 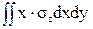, (22)

М_z = 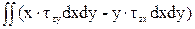. (23)