Полная работа силы на каком-либо перемещении будет
.
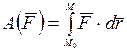Работа силы при вращении твердого тела вокруг неподвижной оси.Разложим силу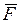 
, приложенную в произвольной точке М тела, по осям 
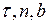естественного трехгранника (рис.2): 
.
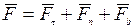Работы составляющих силы по нормали и бинормали равны нулю, ибо они направлены всегда перпендикулярно к вектору скорости точки М.
Поэтому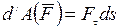 
.
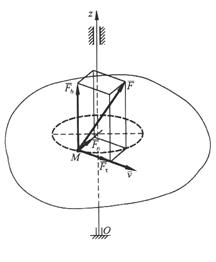Рис.2
Поскольку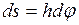 
, то
,
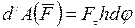где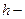 
кратчайшее расстояние от точки приложения силы до оси вращения.
Учитывая, что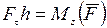 
- момент силы относительно оси 
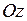, получаем:
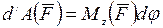
Таким образом, элементарная работа силы, приложенной к какой-либо точке тела, вращающегося вокруг неподвижной оси, равна произведению момента этой силы относительно оси вращения на дифференциал угла поворота тела.
Полная работа
.
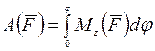В случае, когда момент силы относительно оси вращения тела постоянен, полная работа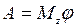 
.
Мощность силы в рассматриваемом случае
,
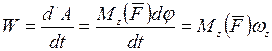где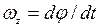 
- проекция на ось 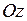угловой скорости.
Работа силы в общем случае движения свободного тела.Скорость точки приложения силы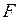 
в рассматриваемом случае равна
,
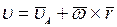где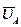 
- скорость полюса А.
Тогда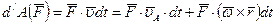 
.
Так как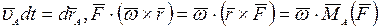 
то
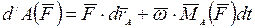, или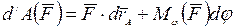 
,
где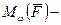 
проекция 
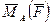на вектор 
; 
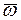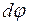- элементарный угол поворота тела вокруг мгновенной оси относительно вращения
Таким образом, элементарная работа силы, приложенной к какой-либо точке твердого тела, в общем случае его движения равна сумме элементарных работ силы на элементарном поступательном перемещении вместе с полюсом и элементарном вращательном перемещении вокруг мгновенной оси, проходящей через полюс.
ГЛОССАРИЙ
| Күштiң элементарлық жұмысы | Элементарная работа силы | Elementary work of force |
| Күш жұмысы | Работа силы | Work force |
| Күш қуаты | Мощность силы | Power of force |
Рекомендуемая литература
Дата добавления: 2016-07-22; просмотров: 1973;