I.3.1 РАБОТА. МОЩНОСТЬ

А. Работа постоянной силы.Работой 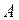постоянной силы 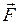называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла 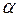между векторами силы 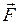и перемещения :

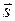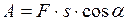. (I.66)

Формула (I.66) показывает, что работа является скалярной величиной и может иметь положительное или отрицательное значение в зависимости от знака косинуса угла .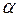

а) б) в)

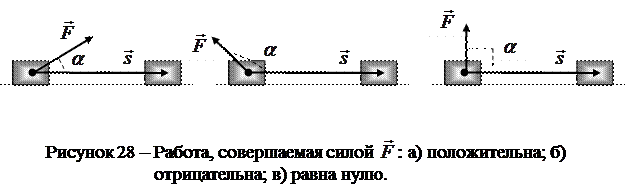
Работа, совершаемая силой 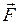, положительна, если угол 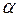между вектором силы 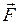и перемещением 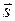меньше 90⁰ (рис.28, а). При значениях угла 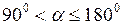работа силы 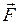отрицательна (рис.28, б). Если вектор силы 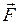перпендикулярен вектору перемещения 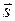, то косинус угла 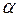равен нулю и работа силы 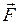равна нулю (рис.28, в).

Если рассмотреть элементарное перемещение 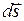, то силу 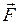можно считать постоянной, а движение точки её приложения – прямолинейным.

Б. Работа переменной силы.Если сила не постоянна по величине, а является функцией перемещения, 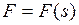, и направлена под углом 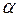к перемещению, то в этом случае надо вводить понятие элементарной работы.

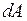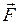Элементарной работой силы на элементарном перемещении 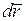материальной точки называется скалярная физическая величина, равная

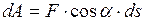. (I.67)

Тогда полная работа на пути от 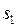до 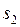находится как:

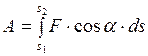. (I.68)

Формула (I.68), показывает, что работа есть интеграл от силы по перемещению.

Из этого утверждения следует, что площадь под кривой на графике зависимости 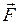от 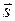(рис.29) равна работе, произведённой данной силой.

Единица работы в системе СИ называется джоулем (Дж).

Джоуль равен работе, совершаемой силой 1Н при перемещении точки её приложения на 1м в направлении действия силы:

1 Дж = 1 Н·м.

В. Работа против силы тяжести.Если тело равномерно поднимается, т.е. движется с постоянной скоростью в направлении, противоположном направлению действия силы тяжести, то над телом совершается работа, равная

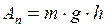, (I.69)

где 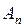- работа по поднятию тела; 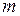- масса тела; 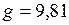м/с² – ускорение свободного падения; 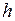- высота, на которую поднимается тело, т.е. перемещение.

Г. Работа против сил трения ( 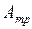).Если тело движется с постоянной скоростью (равномерно) против сил трения, то, над ним совершается работа. При этом сила 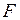совпадает по направлению с перемещением 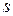и равна по величине силе трения .

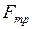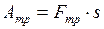. (I.70)

Необходимо отметить, что работа против сил трения превращается в тепловую энергию (одна из форм энергии, связанная с движением атомов, молекул или других частиц, из которых состоит тело.), или говорят, что энергия, затрачиваемая на перемещение тела, диссипирует.

Д. Работа, затрачиваемая на ускорение тела.Если под действием постоянной силы 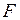тело равноускоренно перемещается на расстояние 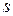, то над ним совершается работа: 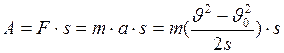. Следовательно,

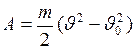, (I.71)

где 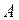- работа, затрачиваемая на ускорение тела, равна разности конечной и начальной кинетических энергий (см. § I.3.3); 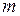- масса тела; 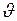- скорость, которую достигает тело; 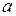- ускорение.

Если ускорение сообщается телу, находящемуся в состоянии покоя ( 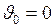), то формула (I.70), примет вид: 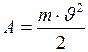. Другими словами, работа, затрачиваемая на ускорение тела равна изменению его кинетической энергии.

Обратите внимание:

§ совершённая над телом работа, запасается в форме кинетической энергии тела (подробнее см. в § I.3.3);

§ из формулы (I.71) видно, что работа, затрачиваемая на ускорение тела, не зависит от характера приложенной к телу силы. Поэтому действующая на тело сила не обязательно должна быть постоянной, а может зависеть от перемещения 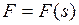или времени .

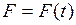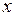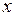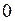Е. Работа, затрачиваемая на упругую деформацию тела.Если пружина растягивается на длину , то действующая на пружину сила возрастает пропорционально от до 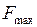. Тогда в формулу для работы 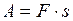следует подставить среднее значение силы 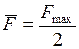. Введём обозначения: 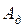- работа против упругой силы, работа по деформации пружины; 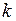- жёсткость пружины; 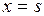- растяжение пружины.

Тогда формула для работы по деформации пружины примет вид:

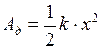. (I.72)

Обратите внимание:

§ работа, затрачиваемая на деформацию (растяжение) пружины, запасается в виде потенциальной энергии растянутой пружины (подробнее см. в § I.3.3).

Для характеристики скорости совершения работы, вводят понятие мощности. Различают среднюю и мгновенную мощности.

Средней мощностью называется скалярная физическая величина, определяемая отношением работы, совершаемой силой или системой сил в течение конечного промежутка времени, к его продолжительности:

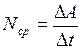. (I.73)

Мощностью (мгновенной мощностью) называется скалярная физическая величина, равная пределу, к которому стремится средняя мощность при бесконечном уменьшении промежутка времени:

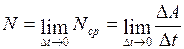. (I.74)

Дадим другое определение мгновенной мощности.

Мощностью (мгновенной мощностью) называется скалярная физическая величина, равная отношению элементарной работы 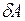к малому интервалу времени 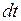, в течение которого эта работа совершается:

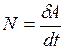. (I.75)

Если материальная точка или тело перемещается со скоростью 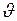, то

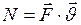, (I.76)

или

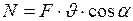, (I.77)

где 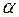- угол между векторам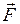и и .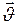

Формула (I.77) показывает, что мощность, развиваемая под действием силы 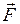, в данный момент времени равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы.

Другими словами, мощность – это работа за единицу времени.

Единица мощности – ватт(Вт): 1 Вт – мощность, при которой за время 1с совершается работа в 1 Дж.

1 Вт = 1 Дж/с.