Дифференциал кинетической энергии механической системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на систему.
Разделим обе части уравнения на 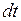 . Тогда:
. Тогда:
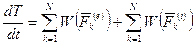 .
.
Таким образом, первая производная по времени от кинетической энергии системы равна сумме мощностей всех внешних и внутренних сил, действующих на точки системы.
Проинтегрировав дифференциальные уравнения, будем иметь:
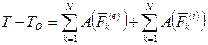 ,
,
где 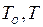 - кинетическая энергия системы в начальном и текущем положениях соответственно;
- кинетическая энергия системы в начальном и текущем положениях соответственно; 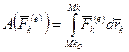 ,
, 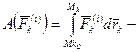 соответственно работа внешней и внутренней силы, действующей на k-ю точку системы.
соответственно работа внешней и внутренней силы, действующей на k-ю точку системы.
Таким образом: изменение кинетической энергии системы при ее перемещении из одного положения в другое равно сумме работ всех внешних и внутренних сил, действующих на систему, на соответствующих перемещениях точек приложения этих сил.
ГЛОССАРИЙ
| Нґктенiң (жүйенiң) кинетикалық энергиясы | Кинетическая энергия точки (системы) | Kinetic energy of particle (system) |
| Нґктенiң (жүйенiң) потенциалдық энергиясы | Потенциальная энергия точки (системы) | Potential energy of particle (system) |
| Толық механикалық энергия | Полная механическая энергия | Total energy |
Рекомендуемая литература
Дата добавления: 2016-07-22; просмотров: 2302;











