Работа силы. Мощность
Работа силы. Мощность
Цель лекции – познакомить с мерой действия силы – работой и мощностью; рассмотреть примеры вычисления работы некоторых сил
План лекции
1. Элементарная и полная работа силы. Пример. Мощность силы
2. Работа силы в различных случаях движения твердого тела
КРАТКОЕ СОДЕРЖАНИЕ ЛЕКЦИИ
Элементарная работа силы. Элементарная работа силы 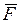 на элементарном перемещении
на элементарном перемещении 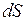 определяется формулой
определяется формулой
 , (1)
, (1)
где  ,
, 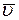 - скорость точки приложения силы.
- скорость точки приложения силы.
Величина 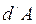 скалярная, ее знак определяется знаком функции
скалярная, ее знак определяется знаком функции 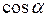 . Если
. Если 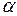 острый угол,
острый угол, 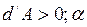 - тупой угол,
- тупой угол, 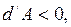 а для
а для 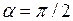 ,
, 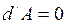 . Так как
. Так как 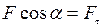 , то формулу (1) можно представить в виде:
, то формулу (1) можно представить в виде:
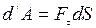 . (2)
. (2)
Таким образом, элементарная работа силы равна произведению элементарного перемещения на проекцию силы на это перемещение.
Поскольку 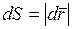 , то, согласно (1)
, то, согласно (1)
 , или
, или 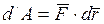 (3)
(3)
Следовательно, элементарная работа силы 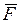 равна скалярному произведению вектора силы и дифференциала радиус-вектора
равна скалярному произведению вектора силы и дифференциала радиус-вектора 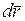 .
.
Так как 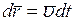 , представим выражение (3) в виде:
, представим выражение (3) в виде:
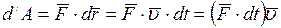 (4)
(4)
Таким образом, элементарная работа силы равна скалярному произведению элементарного импульса силы на скорость точки ее приложения.
В аналитической форме (4) будет иметь вид:
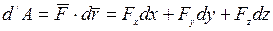
Полная работа силы. Полную работу силы 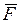 на конечном перемещении определяют как предел суммы ее элементарных работ, т.е.
на конечном перемещении определяют как предел суммы ее элементарных работ, т.е.
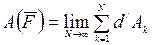 , (5)
, (5)
где  работа силы
работа силы 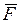 на элементарном перемещении. Так как эта сумма является интегральной суммой определения криволинейного интеграла, то
на элементарном перемещении. Так как эта сумма является интегральной суммой определения криволинейного интеграла, то
 .
.
Используя различные формулы для определения элементарной работы, получаем:
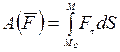 или
или 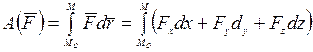 .
.
Если же сила является функцией времени, то, согласно (4), работа силы определяется выражением:
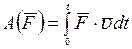 (6)
(6)
Работа силы зависит от характера движения точки приложения силы. Например, если скорость точки приложения силы равна нулю, то 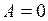 .
.
Пример. Рассмотрим материальную точку М, на которую действует сила тяжести 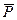 . Точка перемещается из положения М0 в положение М1 , при этом координатные оси выбраны так, что ось z направлена вертикально вверх (рис.1). Проекции силы
. Точка перемещается из положения М0 в положение М1 , при этом координатные оси выбраны так, что ось z направлена вертикально вверх (рис.1). Проекции силы 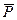 на координатные оси
на координатные оси 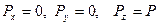 . Подставляя их в формулу для работы, будем иметь:
. Подставляя их в формулу для работы, будем иметь:
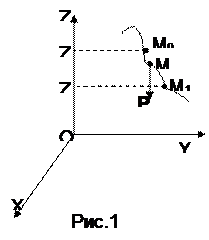
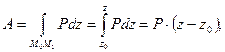 (7).
(7).
Обозначив через h=z-z0 вертикальное перемещение, получим:
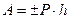 ; (8)
; (8)
или 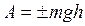 .
.
Следовательно, работа силы тяжести материальной точки равна взятому со знаком плюс или минус произведению модуля силы на вертикальное перемещение точки (при опускании точки работа положительная, при подъеме – отрицательная). Из формулы (8) следует, что работа силы тяжести не зависит от формы траектории, по которой перемещается точка ее приложения.
Единица измерения работы в системе СИ - 1 джоуль 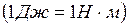 .
.
Мощность. Отношение приращения работы силы к элементарному промежутку времени, за которое оно произошло, называется мощностью:
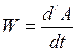 .
.
Так как 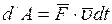 , то
, то 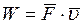 .
.
Таким образом, мощность силы равна скалярному произведению силы на скорость точки ее приложения. Единица измерения мощности в системе СИ - 1 Ватт 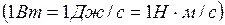 .
.
Работа силы при поступательном движении твердого тела. При поступательном движении твердого тела векторы скоростей, а также элементарные перемещения всех точек тела одинаковы. Тогда элементарная работа силы
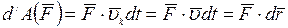 .
.
Дата добавления: 2016-07-22; просмотров: 5767;











