Яблонский А.А. Курс теоретической механики. Ч 2, «Высшая школа», С-Птб.: 2002 и предшествующие издания.
Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. Ч.1 и 2. М., 1961 и последующие издания
Контрольные задания для СРС – 1) Влияют ли внутренние силы системы на изменение ее кинетической энергии? 2) В каких механических системах сумма работ внутренних сил равна нулю?
Лекция 14. Теорема об изменении количества движения
Цель лекции - изложить теорему об изменении количества движения для материальной точки и механической системы
План лекции
Количество движения материальной точки и механической системы. Элементарный и полный импульс силы
Теорема об изменении количества движения
КРАТКОЕ СОДЕРЖАНИЕ ЛЕКЦИИ
Количеством движения материальной точки называется векторная величина, равная произведению массы точки на вектор ее скорости
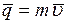 .
.
Количеством движения механической системыназывается вектор 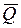 , равный геометрической сумме количеств движения всех точек системы:
, равный геометрической сумме количеств движения всех точек системы:
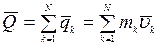
Вектор 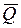 является свободным вектором. Единица измерения в системе СИ – 1кг ∙м/с. Используя понятие центра масс механической системы, количество движения системы представим в виде:
является свободным вектором. Единица измерения в системе СИ – 1кг ∙м/с. Используя понятие центра масс механической системы, количество движения системы представим в виде:
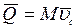 .
.
Элементарным импульсом силы 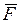 за элементарный промежуток времени
за элементарный промежуток времени 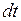 называется векторная величина, равная
называется векторная величина, равная
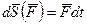 .
.
Полный импульс силы 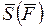 за конечный промежуток времени
за конечный промежуток времени 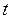 равен:
равен:
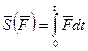 .
.
Единица измерения импульса силы – Ньютон ∙ секунда (Н∙ с).
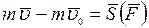 ,
,
где 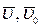 - конечная и начальная скорости точки;
- конечная и начальная скорости точки; 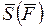 - полный импульс силы за время
- полный импульс силы за время 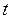 . Это уравнение выражает теорему об изменении количества движения точки: изменение количества движения точки за некоторый промежуток времени равно импульсу действующей на точку силы за этот же промежуток времени.
. Это уравнение выражает теорему об изменении количества движения точки: изменение количества движения точки за некоторый промежуток времени равно импульсу действующей на точку силы за этот же промежуток времени.
Для механической системы будем иметь:
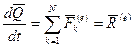 .
.
Это уравнение выражает теорему об изменении количества движения системы в дифференциальной форме: производная по времени от количества движения системы равна геометрической сумме всех внешних сил, действующих на систему.
Умножая обе части уравнения на dt, получим:
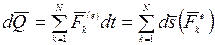 ,
,
т.е., дифференциал количества движения механической системы равен геометрической сумме элементарных импульсов всех внешних сил, действующих на систему.
Интегрируя уравнение в заданных пределах, получим:
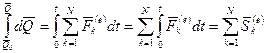 ,
,
или
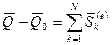 ,
,
где 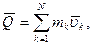
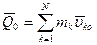 - количества движения системы в начальный и конечный моменты времени.
- количества движения системы в начальный и конечный моменты времени.
Последнее уравнение выражает теорему об изменении количества движения системы в интегральной форме: изменение количества движения системы за какое-либо время равно сумме импульсов всех внешних сил, действующих на систему, за это же время .
Теорема допускает первый интеграл (закон сохранения) в случае, если геометрическая сумма всех внешних сил равна нулю:
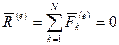 .
.
Тогда вектор количества движения системы будет постоянен по модулю и по направлению: 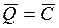 .
.
ГЛОССАРИЙ
| Нүктенiң (жүйенiң) қозғалыс мөлшерi | Количество движения точки (системы) | Momentum of particle (system) |
| Қандай да бiр уақыт аралығындағы күш импульсi | Импульс силы за конечный промежуток времени | Whole force |
Рекомендуемая литература
Дата добавления: 2016-07-22; просмотров: 3259;











