Выбор доверительной вероятности
Доверительная вероятность или надежность Р - это вероятность того, что истинное значение средней генеральной совокупности X попадает в интервал М-tpm<х<М+tpm.
Как правило, минимально допустимая доверительная вероятность, рекомендуемая при определении доверительных интервалов в биологических исследованиях, равна 95% (Р=0,95 или р=1-0,95=0,05), а доверительный интервал оценивается в 5 процентов выборочной средней М:
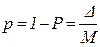 (8),
(8),
где: р - уровень значимости оценок.
Другими словами доверительная вероятность обратно пропорциональна уровню значимости оценок измерений, которая в свою очередь равна ее относительной погрешности. Величина вероятной ошибки не должна превышать величины заданной надежности для проведения данного исследования.
Выбор величины доверительной вероятности является отправной точкой планирования эксперимента. Установив в ходе поискового опыта основные статистические величины изучаемых явлений, как то среднеарифметическую, среднеквадратическое отклонение и др., можно приступать к планированию эксперимента.
Вопросы для самоконтроля.
1. Какова цель проведения поисковых опытов?
2. В чем заключено различие качественного и количественного статистического анализа?
3. Как производится вычисление величин среднего арифметического значения при проведении качественного и количественного анализов?
4. Как производится вычисление значений среднего квадратического отклонения при проведении качественного и количественного анализов?
5. Что характеризует показатель коэффициента вариации выборки.
6. Какую функцию отражает величина средней квадратической ошибки среднего арифметического?
7. Как устанавливается доверительный интервал?
8. Из каких соображений выставляется доверительная вероятность?
Лекция 4. Планирование эксперимента
План лекции
1 Установление заданной надежности
2 Определение количества значимых цифр
3 Определение доверительного интервала с учетом случайных и систематических погрешностей
4 Определение необходимого объема выборки
Установление заданной надежности
При всем разнообразии методов исследовательской работы задача планирования сводится к тому, чтобы при возможно минимальных объемах наблюдений получать достаточно полную информацию об изучаемых объектах. Планирование эксперимента основывается на установленной надежности - Р, которая обеспечивается за счет увеличения количества измерений и уменьшения погрешностей приборов. В некотором смысле эта задача является обратной той, которая решается при статистической обработке результатов поискового эксперимента.
Применяя статистический анализ к решению практических задач, исследователь имеет дело с измерениями биологических объектов. Обычно измерения проводят с точностью до десятых, сотых или тысячных долей единицы. Более точные измерения проводят реже. Как показывает опыт, нет необходимости в точности измерений, когда эта точность практически не нужна. Данное положение относится и к измеряемым объектам, и к вычислениям, обобщающим статистические характеристики. Точность измерений и их последующих вычислений определяется установленной степенью надежности предполагаемых результатов.
Значения заданных надежностей т.е. вероятностей реализаций данных событий - Р представлены в таблице 3.
Таблица 3. Требуемые уровни надежности, связанные с проведением конкретного рода исследования.
| Вероятность заданного уровня Рi | P1 | P2 | P3 | P4 |
| Величина вероятности | 0,68 | 0,95 | 0,99 | 0,999 |
| Уровень вероятности | низкий | средний | повышенный | высокий |
| Уровень значимости оценок – р | 0,32 | 0,05 | 0,01 | 0,001 |
P1 - вероятность приемлемая для поисковых опытов;
P2 - для биологических исследований;
P3,4 - для исследований, связанных со здоровьем человека.
Чтобы избежать грубых ошибок в работе и получить сопоставимые результаты, необходимо неукоснительно соблюдать признанные правила записей и округления приближенных чисел.
Определение количества значимых цифр
Определение количества значимых цифр, то есть установление минимального порядка оперируемых чисел, обеспечивающего заданный уровень надежности, представлено в таблице 4.
Таблица 4. Количество значимых цифр, соответствующих заданному уровню вероятности.
| Вероятность заданного уровня - Pi | P1 | P2 | P3 | P4 |
| Количество значимых цифр – К |
Последний знак значимого числа считается сомнительным и округление возможно только до этого знака. Установленный уровень надежности накладывает условия на общую величину погрешности эксперимента, которая не должна превышать требуемый уровень значимости. Величина погрешности эксперимента обусловлена величинами погрешностей проведенных опытов, которые в свою очередь складываются из ошибок отдельных измерений.
Для установления предельно допустимой величины погрешности эксперимента необходимо определить его общий доверительный интервал и, оценив необходимое количество измерений, которое нужно произвести, понизить погрешность до требуемого уровня значимости.
Определение доверительного интервала с учетом случайных и систематических погрешностей
а) доверительный интервалдля случайных погрешностей De определяется из следующей формулы:
De = tрm (9).
б) доверительный интервал для систематических погрешностейсостоит из отдельных Dq -погрешностей приборов и методов.
Погрешность средства измерения, используемого в нормальных условиях для конкретного прибора, устанавливается посредством данной формулы:
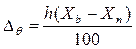 (10),
(10),
где: h - класс точности приборов, Хb - показание верхней границы прибора, Хn - показание нижней границы прибора.
В случае если Хn=0, а Хb= 100, то De = h, то есть класс точности прибора соответствует систематической погрешности в процентах. Для косвенных измерений общая доверительная вероятность будет состоять из ряда частных:
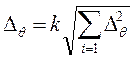 (11),
(11),
где: k - коэффициент, определяемый принятой доверительной вероятностью. Коэффициент k принимают равным 1,1 при доверительной вероятности Р=0.95 [9, 10].
В случае если отношение величин систематической погрешности к случайной 
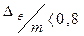 , то не исключенными систематическими погрешностями, по сравнению со случайными, пренебрегают и принимают, что граница погрешности результата равна случайной погрешности D=De. Если же
, то не исключенными систематическими погрешностями, по сравнению со случайными, пренебрегают и принимают, что граница погрешности результата равна случайной погрешности D=De. Если же 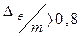 , то случайной погрешностью, по сравнению с систематическими, пренебрегают и принимают, что граница погрешности результата равна систематической погрешности D=Dq.
, то случайной погрешностью, по сравнению с систематическими, пренебрегают и принимают, что граница погрешности результата равна систематической погрешности D=Dq.
При проведении измерений предпочтительно регистрировать не только полученные абсолютные значения исследуемых параметров аi, но и в отдельных случаях переводить их в относительные величины. Относительные показатели дают возможность сопоставлять измеренные величины, имеющие различные размерности, как это показано в нижеприведенных формулах, и переходить к относительной системе координат. Например, подобным образом осуществлена оценка влияния индивидуальных свойств деконсервированных ооцитов и эмбрионов млекопитающих на уровень их сохранности и установлен верхний порог данного показателя [8].
Элементарная логика и практический опыт показывают, что не разумно стремиться к неоправданно большому числу испытаний, если убедительный результат можно получить при минимально допустимом объеме выборки.
Установленная надежность накладывает условия на общую величину погрешности эксперимента, которая не должна превышать требуемый уровень значимости. Общая величина погрешности эксперимента состоит из погрешностей, возникающих при проведении отдельных опытов, которые складываются из ошибок отдельных измерений. Для установления предельно допустимой величины погрешности эксперимента необходимо определить его общий доверительный интервал и, оценив необходимое количество измерений, понизить величину погрешности до требуемого уровня значимости. Выбор величины доверительной вероятности является отправной точкой планирования эксперимента. Установив в ходе поискового опыта основные статистические величины изучаемых явлений, такие как среднее арифметическое и среднеквадратическое отклонение, можно приступать к планированию эксперимента.
Вопросы для самоконтроля.
1. Какие факторы влияют на выбор уровня надежности?
2. От чего зависит количество значимых цифр в числе с которым производятся требуемые операции?
3. Как определить доверительный интервал для случайных и систематических погрешностей?
4. Какие существуют особенности соотношения довирительных интервалов для случайных и систематических погрешностей?
5. Из каких составляющих состоит общая величина погрешности эксперимента?
Дата добавления: 2020-10-14; просмотров: 1184;











