Графическое представление экспериментальных данных

Современную статистическую науку невозможно представить без применения графиков. Они стали средством научного обобщения. Выразительность, доходчивость, лаконичность, универсаль­ность, обозримость графических изображений сделали их незаменимыми в исследовательской работе и в международных сравнениях и сопоставления социально-экономических явлений.

Значение графического метода в анализе и обобщении данных велико. Графическое изображение, прежде всего, позволяет осуществить контроль достоверности статистических показателей, так как представленные на графике, они более ярко показывают имеющиеся неточности, связанные либо с наличием ошибок наблюдения, либо с сущностью изучаемого явления. С помощью графического изображения возможно изучение закономерностей развития явления, установление существующих взаимосвязей. Простое сопоставление данных не всегда дает возможность уловить наличие причинных зависимостей, в то же время их графическое изображение способствует выявлению причинных связей, в особенности, в случаях установления первоначальных гипотез, подлежащих затем дальнейшей разработке. Графики также широко используются для изучения структуры влияний, их изменения во времени и размещения в пространстве. В них более выразительно проявляются сравниваемые характеристики и отчетливо видны основные тенденции развития и взаимосвязи, присущие изучаемому явлению или процессу.

Таким образом, графики дают возможность наблюдать закономерности изменения функций как на плоскости, так и в пространстве, тем самым наглядно показывают закон изменения С=f (а_i). Обычно на абсциссе откладывают значение аргументов, по ординате - значение функций. Общие правила для выбора масштаба: кривые по возможности располагают наклонно к осям координат (около 45⁰); результирующую, или основную, кривую вычерчивают на всем листе, начало отсчета не обязательно размещать в пределах листа. Желательно, чтобы наименьшее деление масштаба графика соответствовало абсолютной ошибке измерений. Тогда ошибка отсчета по графику не будет превышать ошибки измерений.

Общий вывод для исследователя таков - в ходе исследования необходимо пользоваться таблицами и построенными по ним графиками; в тексте отчетов по исследованию нужно помещать преимущественно графики, перенося значительную часть табличного материала в приложения.

Проведение ковариационного анализа

Предыдущие главы были посвящены методам изучения закономерностей в варьировании отдельных признаков и свойств в пределах одной совокупности, и только при сравнении двух распределений учитывали средние и ошибки двух выборок. Однако в последнем случае характеристики сравниваемых совокупностей были получены для каждой из них независимо от причин, обуславливающих то или иное значение каждого наблюдения. В практике биологических исследований часто возникает необходимость изучить характер связи между двумя (или более) варьирующими признаками.

Ковариационный анализ направлен на установление сопряженности вариационных связей и объединяет в себе ряд относительно самостоятельных методов: дисперсионный, корреляционный и регрессионный анализы.

1) Дисперсионный анализ:

Р.Фишер в 1925 году предложил метод комплексной оценки сравниваемых средних, получивший название дисперсионного анализа. Этот метод основан на разложении общей дисперсии статистического комплекса на составляющие ее компоненты (отсюда и название метода), сравнивая которые друг с другом посредством F-критерия, можно определить, какую долю общей вариации учитываемого (результативного С_i) признака обуславливает действие на него как регулируемых а_i , так и не регулируемых в опыте факторов b_i, d_i.

Ценность этого метода заключается в том, что он позволяет выявить суммарное действие факторов, действие каждого регулируемого в опыте фактора в отдельности и действие различных сочетаний факторов друг с другом на результативный признак.

Достоверность влияния а_i фактора устанавливается таким образом:

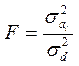(16а),

где: s_аi - дисперсия а_i фактора, а s_d - дисперсия неучитываемых факторов.

Если F 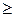F_st, то наличие связи считается установленным. Достоверность различия между двумя факторами а₁ и а₂ устанавливается аналогичным образом, используя критерий Фишера F_st (см. приложение табл. 3).

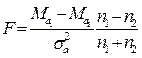(16б).

После того как достоверно установлено действие регулируемого фактора а_i, можно измерить силу его влияния на результативный признак (С) (метод Плохинского).

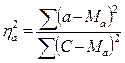(19),

где: 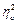- сила влияния а-го фактора на величину целевой функции.

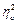=r², где: r² - коэффициент детерминации, а r - корреляция.

2) Корреляционный анализ:

При изучении живых организмов редко приходится встречаться с так называемой функциональной зависимостью (r=1), при которой каждому значению одной переменной - аргументу соответствует тоже одно, вполне определенное значение другой переменной - функции.

Растения, животные и микроорганизмы в процессе развития постоянно взаимодействуют с факторами внешней среды, изменяясь под влиянием разнообразных условий существования. Поэтому у них связь между признаками проявляется в виде так называемой корреляционной зависимости, или корреляции. Эта форма связи характерна тем, что каждому значению одного признака соответствует не одно, а несколько значений другого признака, то есть его распределение.

Задача исследования корреляционной связи - определить характер и измерить тесноту сопряженности между признаками, из которых один является факториальным а_i , а второй результативным С.

Простейшим способом представления коэффициента корреляции является аналитическое выражение его с использованием критериев Стьюдента.

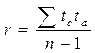(20).

Если r<0,5, то корреляция считается слабой и, наоборот, если r>0,6, то сильной.

3) Регрессионный анализ:

Зависимость между переменными величинами а_i и С может быть описана разными способами. В частности, любую форму связи можно выразить уравнением общего вида С=f(а_i), где С рассматривают в качестве зависимой переменной, или функции от другой - независимой переменной величины а_i, называемой аргументом. Соответствие между аргументом и функцией может быть задано таблицей, формулой, графиком и т.д. Изменение функции, в зависимости от изменений одного или нескольких аргументов, называется регрессией. Для выражения регрессии служат корреляционные уравнения, или уравнения регрессии, эмпирические или теоретические вычисленные ряды регрессии, их графики, называемые линиями регрессии, а также коэффициенты линейной и нелинейной регрессии.

Различных форм и видов корреляционных связей много. Задача сводится к тому, чтобы в каждом конкретном случае выявить форму связи и выразить ее соответствующим корреляционным уравнением, что позволяет предвидеть возможность изменения одного признака С на основании известных изменений другого а, связанного с первым корреляционно.

Общая форма уравнения регрессии выглядит таким образом:

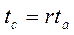(21).

Обработка экспериментальных данных при помощи ковариационного анализа является достаточно трудоемкой операцией и без применения вычислительной техники зачастую не реализуемая. В настоящее время существует достаточно большое количество прикладных программ, позволяющих обрабатывать экспериментальные данные с выражением функциональных зависимостей в виде формул.

Применение регрессионного анализа дает возможность экспериментаторуиспользовать методы проведения активного эксперимента, то есть применять методы организации совокупности опытов с различными условиями для получения наиболее достоверной информации о свойствах исследуемого объекта при наличии случайных неконтролируемых возмущений. Величины, определяющие условия данного опыта, обычно называют факторами (напр., температура, концентрация), а их совокупность - факторным пространством. Набор значений факторов характеризует некоторую точку факторного пространства, а совокупность всех опытов составляет так называемый факторный эксперимент. Расположение точек в факторном пространстве определяет план эксперимента, который задаёт число и условия проведения опытов с регистрацией их результатов.

Планирование эксперимента используют для изучения и математического описания процессов и явлений посредством построения математических моделей (в форме так называемых уравнений регрессии) – соотношений, связывающих с помощью ряда параметров значения факторов и результаты эксперимента, называемых откликами. Основное требование, предъявляемое к планам факторного эксперимента, в отличие от пассивного эксперимента, - минимизация числа опытов, при которой получают достоверные оценки вычисляемых параметров при соблюдении приемлемой точности математических моделей в заданной области факторного пространства. В этом случае задача обработки результатов факторного эксперимента заключается в определении численных значений указанных параметров.

Провидение эксперимента при поиске оптимальных условий

Поиск оптимальных условий является одной из наиболее распространенных научно-технических задач. Они возникают в тот момент, когда установлена возможность проведения процесса и необходимо найти наилучшие (оптимальные в некотором смысле) условия его реализации.

Формализация позволяет использовать преимущества, содержащиеся в применении развитого математического аппарата. Их не мало. Легкость и четкость формулировки основных результатов. Вывод всех следствий, которые представляют интерес. Однозначность и определенность суждений. Количественные оценки. Кроме того, возможность применения аппарата планирования эксперимента со всеми присущими ему известными преимуществами, в том числе и с возможностью минимизации числа опытов, оценки неопределенности в результатах, сопоставимости и преемственности работ и т.д.

Но когда экспериментатор делает попытку познакомиться с планированием эксперимента, он часто сталкивается с серьезными трудностями. Больше того, иногда он просто не верно применяет методы планирования или выбирает не самый оптимальный для данной ситуации путь исследования, или допускает еще какие-нибудь досадные ошибки. При этом снижается эффективность его работы и появляется опасность дискредитации важного и полезного направления.

Поиск оптимальных условий, построение интерполяционных формул, выбор существенных факторов, оценка и уточнение констант теоретических моделей (например, кинетических), выбор наиболее приемлемых из некоторого множества гипотез о механизме явлений, исследование диаграмм состав-свойство – вот примеры задач, при решении которых применяется планирование эксперимента. Можно сказать, что там, где есть эксперимент, имеет место и наука о его проведении – планирование эксперимента.

Планирование экстремального эксперимента – это метод выбора количества и условий проведения опытов, минимально необходимых для отыскания оптимальных условий, т.е. для решения поставленной задачи. Путь к вершине довольно извилист. Он становится еще более трудоемким при возрастании числа независимых переменных. Наиболее короткий путь к вершине – направление градиента функции отклика. Градиент непрерывной однозначной функции 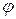есть вектор:

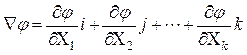(23),

где: 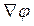- обозначение градиента, 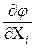- частная производная функции по i – му фактору, i, j, k – единичные векторы в направлении координатных осей.

Следовательно, составляющие градиента суть - частные производные функции отклика, оценками которых являются коэффициенты регрессии. Изменяя независимые переменные пропорционально величинам коэффициентов регрессии, происходит движение в направлении градиента функции отклика по самому крутому пути. Поэтому процедура движения к почти стационарной области называется крутым восхождением.

Таким образом, крутое восхождение – это движение в направлении градиента функции отклика. Градиент задается частными производными, а частные производные функции отклика оцениваются коэффициентами регрессии. В крутом восхождении независимые переменные изменяют пропорционально величинам коэффициентов регрессии и с учетом их знаков. Составляющие градиента однозначно получаются умножением коэффициентов регрессии на интервалы варьирования по каждому фактору. Серия опытов в направлении градиента рассчитывается последовательным прибавлением к основному уровню факторов величин, пропорциональных составляющим градиента.

Реализацию мысленных опытов для адекватной модели начинают с опыта, условия которого выходят за область эксперимента хотя бы по одному из факторов. Для неадекватной модели один-два опыта выполняют в области эксперимента. Возможно проведение сразу всех мысленных опытов. Более экономная процедура состоит в проведении двух-трех опытов, оценке результатов и принятии решений о прекращении или дальнейшем проведении экспериментов (последовательный поиск). При движении по градиенту возникают различные ситуации, определяющие принятие дальнейших решений.

Вопросы для самоконтроля.

1 Перечислите последовательность обобщения полученных экспериментальных данных.

2 Каким образом устанавливаются функциональные связи?

3 Какова необходимость проведения дисперсионного анализа?

4 Какова необходимость проведения корреляционного анализа?

5 Какова необходимость проведения регрессионного анализа?

6 Как производится поиск оптимальных условий проведения эксперимента?