Лекция 3. Проведение поисковых опытов
План лекции
1. Статистический анализ
2. Вычисление среднего арифметического
3. Установление среднего квадратического отклонения
4. Нахождение доверительного интервала
Статистический анализ
Целью поисковых опытов может быть проверка отдельных частей разработанной методики и приспособленности приборов тем измерениям, которые определила методика. Поисковые опыты необходимо ставить для того, чтобы найти основание для расчета количества опытов.
Классические работы Р. Фишера открыли новую страницу в истории биометрии. Они показали, что планирование эксперимента и обработка результатов - это две тесно связанные между собой задачи статистического анализа.
Статистический анализ, в свою очередь, подразделяется на количественный и качественный, в зависимости от законов, описывающих изучаемый признак [7]. Здесь и далее в левой части страницы будет изложен материал количественного статистического анализа, в правой - качественного. На полной странице будет представлена информация, общая для обоих методов.
Статистический анализ:
| Количественный | Качественный |
| основанный на нормальном законе распределения признаков и имеющий количественную градацию | основанный на биноминальном распределении признаков и не имеющих количественных градаций (метод альтернативного варьирования). |
Задачей статистического анализа является оценка наиболее вероятного значения определяемой величины среднего арифметического М (вероятности W), а также определение соответствующей ошибки средней m и вероятность ее появления Р.
Вычисление среднего арифметического
Величина средней арифметической является центром распределения, вокруг которого группируются текущие значения изучаемого признака.
Из нормального закона распределения ошибок явствует, что наиболее вероятным значением измеряемой величины будет среднее арифметическое М из полученных результатов. Оно определяется как сумма всехизмерений, деленная на их количество n:
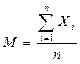 (3), где: Хi - варианта (текущее значение изучаемого параметра), n – количество вариантов (объем выборки), i – индекс текущей переменной. (3), где: Хi - варианта (текущее значение изучаемого параметра), n – количество вариантов (объем выборки), i – индекс текущей переменной.
| Вероятностью W какого-либо события называют в математике отношение числа случаев, при которых это событие произошло n0, к общему числу наблюдений n:
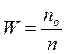 (3а). (3а).
|
Средние величины не являются универсальными характеристиками варьирующих объектов. При одинаковых средних величинах признаки могут отличаться по величине и характеру варьирования. Поэтому наряду со средней для характеристики варьирующих признаков используют и показатели вариации. Одним из таких показателей является среднее квадратическое отклонение.
Установление среднего квадратического отклонения
Для оценки изменчивости вариационного ряда введена единица изменчивости всех вариант - стандартное отклонение s, которую вычисляют следующим образом:
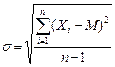 (4),
(4), 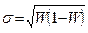 (4а).
(4а).
Характерной особенностью s как оценки изменчивости является то, что она не может быть постоянной величиной, ее рассчитывают непосредственно для каждого вариационного ряда. Преимущество данной величины перед другими показателями вариации состоит в том, что она распадается на составные компоненты, позволяя тем самым оценивать влияние различных факторов на величину учитываемого признака, а также служит критерием равноточности измерений.
Определение величины коэффициента вариации Сv
При изучении биологических систем часто возникает необходимость сравнить изменчивость разных биологических показателей, выраженных в несопоставимых величинах. С этой целью используют коэффициент вариации, который представляет собой отношение среднего квадратического отклонения к среднему арифметическому, выраженное в процентах.
 (5).
(5).
Этот показатель можно использовать для оценки биологических процессов, исходя из того, что более стабильная система с меньшим коэффициентом вариации более важна для организма и, кроме того, требует меньшее количество измерений для получения достоверных результатов. Принято считать степень вариабельности низкий, если СV<10%, средний, если СV>10%, но меньше 25% и высокий, если СV>25%.
Дата добавления: 2020-10-14; просмотров: 588;











