Лекция 5. Определение необходимого объема выборки
План лекции:
1 Определение минимального количества измерений, обеспечивающего достоверный научный результат для одной выборки.
2 Определение минимального количества измерений, обеспечивающего достоверный научный результат при сравнении двух выборок
3 Формулы приближенной оценки статистических показателей
Определение минимального количества измерений, обеспечивающего достоверный научный результат для одной выборки
При всем разнообразии методов исследовательской работы задача планирования эксперимента сводится к тому, чтобы при возможно минимальных объемах наблюдений получать достаточно полную информацию об изучаемых объектах. Планирование эксперимента основывается на установленной надежности, которая обеспечивается за счет увеличения количества измерений и уменьшения их погрешностей. Представленные в литературе формулы оценки оптимального числа измерений имеют значительные численные расхождения [6, 7, 11]. Очевидно, что данные расхождения объясняются допущениями, вводимыми авторами в ходе вывода конечных формул. Количественная взаимосвязь представленных параметров выражена в предлагаемых формулах.
Оптимальная схема исследования основана на проведении минимального количества измерений при обязательном условии получения достоверного результата. Необходимая численность выборки - n, отвечающая точности получения среднего результата, зависит от величины ошибки выборочной средней и выводится из формулы вычисления средней квадратической ошибки среднего арифметического т формулы (6) [1, 2, 3].
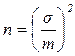 (6а),
(6а),
где: s - среднее квадратическое отклонение, откуда домножив и разделив данное выражение, приведенное в скобках, на среднюю величину - М и критерий Стьюдента - t, произвели замену второго сомножителя на р-1, и третьего сомножителя на коэффициент вариации - Сv.
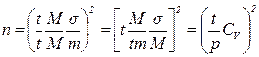 (12).
(12).
Для уровня надёжности Р=0,95 и величины критерия Стьюдента t=2, соответствующего достоверной выборке (n³30), значение формулы упрощается:
n=0.16  (12а).
(12а).
Значения численности выборки, основанной на нормальном законе распределения признаков и имеющей количественную градацию в зависимости от коэффициента вариации при уровне надёжности Р=0,95,представлены в таблице 5.
Таблица 5. Значение минимального объема выборки n в зависимости от коэффициента вариации для количественного анализа при P=0,95
| Cv,% | |||||||||
| n |
Пример. В случае если величина среднеквадратического отклонения исследуемого нами признака равна пяти (s=5), а среднее арифметическое двадцати (М=20), коэффициент вариации для данной выборки составляет двадцать пять процентов (Сv=(5/20)100=25%). Тогда минимальное количество измерений, обеспечивающее достоверный результат с уровнем надежности 0,95, равно сто (n=0.16´252 =100). Относительная погрешность измерения соответствует поставленному критерию надежности.
При альтернативной группировке данных, основанных на биномиальном распределении признаков и не имеющих количественных градаций, когда численность выборочных групп выражается в долях единицы, планируемый объем наблюдений определяется следующим образом:
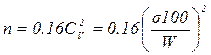 (12б),
(12б),
где: W-вероятность, величина, определяемая как отношение числа случаев N0, при которых это событие произошло, к общему числу наблюдений N:
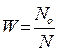 , и
, и 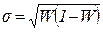 [3, 7], тогда:
[3, 7], тогда:
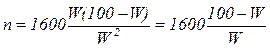 (12в).
(12в).
Для выборки, основанной на биномиальном законе распределения признаков и не имеющей количественной градации, при уровне надёжности 0.95, оптимальное количество измеренийпредставлено в таблице 6.
Таблица 6. Значение минимального объема выборки n в зависимости от средней вероятности W, для качественного анализа при Р=0.95.
| W (%) | ||||||||
| n |
Пример. В случае если вероятность изучаемого нами признака составляет восемьдесят пять процентов (W=85%), то величина среднеквадратического отклонения для данной выборки составит около тридцати шести измеряемых единиц (s=35,7). Таким образом, необходимо провести не менее двухсот восьмидесяти пяти измерений, чтобы получить достоверный результат с заданным уровнем надёжности (n=1600(15/85)=285).
Обобщая полученные результаты, можно сделать следующее заключение: для уменьшения ошибки выборочной средней в К раз нужно увеличить объем выборки в К2 раз. Если величина количества измерений, обеспечивающего требуемую достоверность значения, настолько велика, что её невозможно реализовать на практике, то в отдельных случаях следует планировать опыт, основываясь на оценке достоверности различия средних значений контроля и эксперимента.
Определение минимального количества измерений, обеспечивающего достоверный научный результат при сравнении двух выборок.
Минимальное количество измерений, обеспечивающих достоверный результат, зависит от выбора метода проведения статистического анализа и от способа проверки полученного результата. Если полученный результат планируется сравнивать с данными, полученными в контроле при выполнении данного эксперимента, то необходимое количество измерений (nD) в каждой выборке можно определить из следующей формулы ф(17):
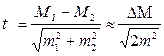 ,
, 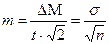 ,
, 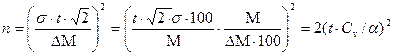 ,
,
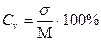 ,
, 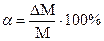 , nD= 2 (t СV /a)2 (13),
, nD= 2 (t СV /a)2 (13),
где: СV – коэффициент вариации выборки, a - относительный показатель расхождения средних величин сравниваемых выборок, t – критерий Стьюдента {1,00; 1,66; 1,98; 2,63} для уровней надежности Р{0,68; 0,90; 0,95; 0,99} при допустимых величинах погрешности вычисления р{0,32; 0,10; 0,05; 0,01}, соответственно. Данная формула ф(13) позволяет установить минимальное количество измерений по каждой из сравниваемых выборок.
Значимая вариация биологических параметров (СV³10%) приводит к необходимости проведения большого количества повторов измерений (n) с целью получения достоверного результата (рис. 1). Если для количественного метода статистического анализа, как правило, достаточно малой выборки (n£30 для СV»10¸15%), то для качественного (метод альтернативного варьирования) количество повторов необходимо значимо больше (n³100 для СV»35¸300%, при вероятности полученного результата М»90(10)¸50%, соответственно) (рис. 2).
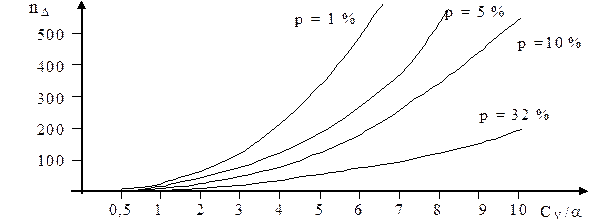
Рис. 1. Зависимость минимального количества измерений, необходимых для получения достоверности различия двух сравниваемых выборок, от соотношения показателей коэффициента вариации (СV) и относительного показателя расхождения средних величин сравниваемых выборок (a) при различных допустимых величинах погрешности вычисления (р).
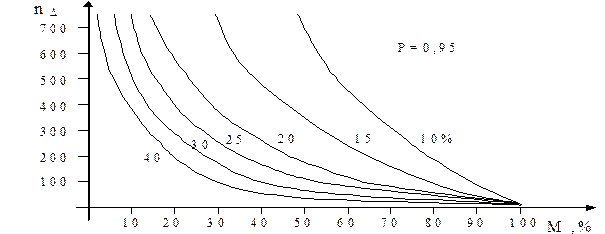
Рис. 2. Зависимость минимального количества измерений, необходимых для получения достоверности различия двух сравниваемых выборок, от относительного показателя расхождения средних величин сравниваемых выборок (a) при различной вероятности реализуемого события (М) (метод альтернативного варьирования при уровне надежности 0,95).
При общепринятом в биологии уровне надежности (Р³0,95), когда допустимая величина погрешности вычисления не должна превышать пять процентов (р=5%) формулы упрощаются:
nD= 8(СV /a)2 (13а), n = 0,16CV2 (13б).
Это условие особенно важно соблюдать, в случае если различие между сравниваемыми выборками составляет больше семи процентов (a>7, nD<n).
Поскольку среднеквадратическое отклонение (s) при использовании метода альтернативного варьирования зависит от средней величины (М), то необходимое количество измерений связано с данным параметром, который может изменяться от 0 до 100% (рис 3).
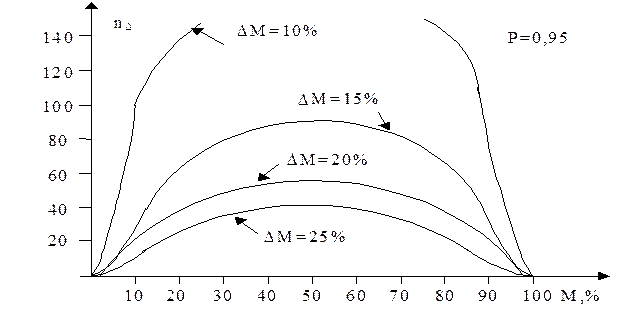
Рис. 3. Зависимость минимального количества измерений, необходимых для получения достоверности различия двух сравниваемых выборок, от показателя расхождения средних величин сравниваемых выборок (DМ) при различной вероятности реализуемого события (М) (метод альтернативного варьирования при уровне надежности 0,95).
Формулы приближенной оценки статистических показателей
Дата добавления: 2020-10-14; просмотров: 672;











