Лекция 6. Проведение эксперимента

План лекции:

1 Соблюдение условий равноточности измерений

2 Вычисление средней взвешенной величины и ее ошибки

3 Сравнение средних значений для определения существенности различия между двумя вариационными рядами

4 Определение нормированного отклонения

Соблюдение условий равноточности измерений

При разработке рабочей гипотезы устанавливают факторы, определяющие развитие явления. Иначе говоря, устанавливают независимые переменные (аргументы а_j, b_j), определяющие изменение зависимой переменной функции С ф(1). Исследователь, наблюдая в опыте за развитием явления при воздействии факторов, получает материал или данные исследования.

В опытах измеряют или отмечают величины и качественные показатели, характеризующие как факторы (аргументы а_j, b_j), так и показатели развития явления (целевую функцию С).

Изучение суммарного влияния многих количественно неопределенных факторов, сочетающихся в произвольных и непонятных для исследователя соотношениях, часто приводит к неясным закономерностям и ошибочным выводам. В таких случаях следует все факторы, обуславливающие явления, разделить на основные а_j, b_j , оказывающие наибольшее влияние на развитие явления, и дополнительные d_j, влияющие на развитие явления второстепенно. Тогда в опыте измеряют или отмечают лишь величины и свойства, характеризующие основные факторы [14].

Чтобы устранить или, по крайней мере, уменьшить ошибку, появляющуюся вследствие деления основных факторов на а_j - поддающиеся изменениям в ходе эксперимента и b_j - не поддающиеся, надо при постановке опытов стремиться нейтрализовать вариацию b_j факторов. То есть создать такие условия, при которых действия b_j факторов было бы возможно более неизменно и незначительно, а величины и свойства, характеризующие эти факторы, приближались бы к постоянным. При этом исследователь должен стремиться сделать переменными величинами лишь a_j факторы. Таким образом, общим принципом исследования является постоянство всех остальных факторов при изменении избранных a_j. Тестом на соблюдение выше перечисленных условий является критерий равноточности измерений.

Измерения, дающие дисперсии одинаковой величины, называются равноточными. Равноточность измерений серии опытов позволяет обобщить обработку результатов экспериментов и уменьшает суммарные ошибки исследования. Практически добиться равноточности измерений можно только в тех случаях, когда измерения будет проводить достаточно опытный человек одним и тем же прибором в одинаковых условиях.

Условием равноточности опытов является критерий Фишера F, который определяется из таблиц (см. приложение, табл. 3.).

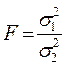(16),

где: s₁ и s₂ - среднеквадратические отклонения разных серий опытов, s₁ 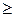s₂.

В случае если вычисленное значение критерия Фишера окажется меньше или равным табличному (F 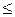F_Т), то результаты считаются равноточными. В некоторых случаях неравноточность приводит к несравнимым результатам, к ошибочным выводам и заключениям, поэтому надо всегда добиваться равноточности измерений исследуемых величин. Для избежания получения искажения объективной информации также необходимо исключить грубые ошибки, которые возникают при проведении измерений.

Обобщение результатов эксперимента, полученных в различных опытах, проводят при помощи вычисления средневзвешенной величины и ее ошибки.

Вычисление средней взвешенной величины и ее ошибки

Если каждое значение варьирующего признака представлено в вариационном ряду не одним, а несколькими наблюдениями, и при этом условие равноточности опытов соблюдено, то формула для вычисления средней арифметической заменяется взвешенной средней. При объединении групповых средних их весами будут объемы групп n_i, по которым эти средние вычислены. Общую (взвешенную) среднюю арифметическую и ее ошибку нескольких однородных групп определяют по формуле:

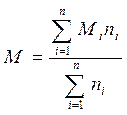
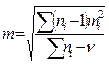(3б), (6б),

где: n - число независимых выборочных групп.

Выражения для вычисления средней взвешенной позволяют использовать литературные данные (при условии выполнения выше изложенных условий), что существенно может облегчить обеспечение требуемой достоверности результатов. В случае, если исследователь наблюдает расхождение двух величин целевых функций С ф(1), полученных при измерении изучаемых факторов а_i, то достоверность данного расхождения можно подтвердить при помощи критерия Стьюдента.

Сравнение средних значений для определения существенности Различия между двумя вариационными рядами

Для выяснения вопроса о случайном или неслучайном расхождении значений некоторого параметра проводят две серии экспериментов и для каждой из них подсчитывают средние значения М₁ и М₂. Если между ними есть различие, то можно допустить два равновероятных объяснения. Первое - предположив, что обнаруженная разность обуславливается случайным варьированием средних величин исследуемой выборки около некоторой общей, хотя и неизвестной нам в точности генеральной средней. Тогда найденные средние должны считаться принадлежащими к одной и той же качественно однородной совокупности. Второе - рассматриваемые две средние величины принадлежат к двум качественно отличным друг от друга статистическим совокупностям. Оба эти предположения одинаково законны и применимы ко всякой паре сравниваемых величин М.

Для оценки существенности различий между двумя средними существует следующая формула:

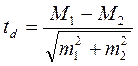(17),

которая справедлива для больших выборок (n>30) или для равновеликих вариационных рядов (n₁»n₂) малых выборок.

Для определения существенности различий необходимо обращаться к таблице Стьюдента (см. прилож. табл. 7). По найденному значению t_d и числу степеней свободы k=n₁+n₂ -2 в таблице 7 находим соответствующее значение вероятности Р.

Как уже отмечалось, в биологических экспериментах принято, чтобы показатель надежности был не менее 95% (Р 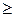0,95 или Р≤0,05 ). Если полученное различие меньше, к примеру, 80...90%, то необходимо высказываться с меньшей категоричностью. Можно указать, что разность может иметь место, но в данной серии экспериментов она не доказана, и необходимо поставить дополнительные опыты.

Зачастую перед исследователем встает задача установить величину отклонения от средней величины конкретного текущего значения (говоря иными словами, степень выраженности, “индивидуальности” данного значения) с последующим сопоставлением ее с другой величиной расхождения из другой выборки, которая, возможно, имеет иную размерность. Данное сравнение можно производить при помощи нормированного отклонения (критерия Стьюдента).

Определение нормированного отклонения

Многие наблюдаемые явления подчиняются приблизительно нормальному закону распределения. По этой причине основная часть классической статистической теории предполагает нормальность рассматриваемой случайной величины. Важным теоретическим результатом относительно выборочных распределений является центральная предельная теорема. Вот одно из важных применений этой теоремы: если мы получаем случайную выборку объема n из генеральной совокупности с конечной дисперсией, то независимо от распределения нашей случайной величины Х распределение выборочного среднего М при больших n будет приблизительно нормальным [12].

Один из самых простых способов определения нормальности распределения выборки представляет собой вычисление коэффициентов асимметрии А_s и эксцесса Е_х (см. приложение, табл. 1.). Соблюдения условия нормальности распределения выборки позволяет использовать как все представленные в данной работе формулы, так и установление величины нормированного отклонения.

Отклонение той или иной варианты от средней арифметической, отнесенной к величине среднего квадратического отклонения, называют нормированным отклонением:

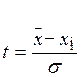(18).

Этот показатель позволяет "измерять" отклонение отдельных вариант от среднего уровня и сравнивать их для разных признаков. Иными словами, он характеризует индивидуальность признака и позволяет установить сопряженность связей между аргументами и величиной целевой функции. Так же оценку нахождения и развития любой как физической так и биологической системы можно произвести при помощи нормируемого отклонения (критерия Стьюдента – t). При t=±1 состояние системы находится в оптимуме - opt, t=+1¸+2 - supopt состояние, t=-1¸-2 - subopt состояние, t=+2¸+3 -suppat состояние, t=-2¸-3 - subpat состояние.

Например, проведем сравнительный анализ существующих технологий криоконсервации биообъекта. Полагаем, что центральная теорема статистики утверждающая, что всякое распределение стремится к нормальному при повышении количества измерений, может служить методологическим постулатом целесообразности выбора приоритетности развития изучаемого явления. Различные направления исследований являются теми факторами, которые расширяют диапазон и приводят генеральное распределение к нормальному. Только та система будет развиваться, рост которой сбалансирован противоположно дополняющими началами. Односторонность развития приводит к обратным явлениям: деградации и распаду на отдельные составляющие гармоники общего распределения системы. Условия равновесия развития будут выполняться только тогда, когда система соответствует нормальному закону распределения составляющих её гармоник. И как следствие, приоритетность развития каждой из них должна соответствовать весу её плотности вероятности распределения в общей генеральной совокупности (рис. 4).

Величина вероятности распределения каждой из гармоник P(t), в нашем представлении, является прямым аналогом приоритетности направления изучаемого явления для любой из составляющих генеральной совокупности, t - количественный показатель степени отклонения конкретной гармоники от условно оптимального состояния целостной генеральной совокупности. Отрицательные гармоники (t = -1, -2) - показатели субоптимальности режимов, а положительные - супероптимальности. Представленные на графике численные значения не обязательно должны быть целыми величинами, они могут принимать любые значения. Чем ближе к нулевому (равновесному) состоянию расположена гармоника, тем она ближе к оптимуму и, следовательно, большим приоритетом должна обладать.

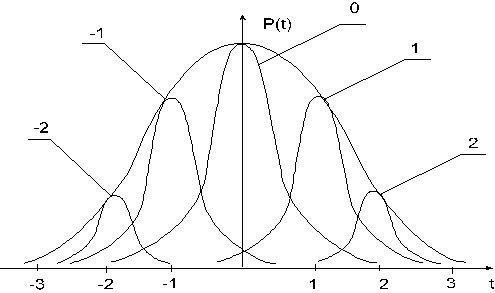
Рис.4. Стандартизованная форма нормальной кривой генерального распределения, включающего спектр отдельных составляющих его гармоник. P(t) - функция плотности вероятности распределения изучаемого явления; t - нормируемое отклонение (критерий Стьюдента); 0, ±1, ± 2 - отдельные составляющие гармоники, характеризующие направления исследования.

Адекватная оценка изучаемого явления требует проведения полного и всестороннего анализа с учётом всех его качеств и характеристик. Проведение объективного анализа возможно при наличии обобщающего фактора, который позволяет не только уравновесить, но и сгладить противоречия.

Ускорение процессов развития организма и создание новых видов растений и животных, которые не существуют в живой природе, волнуют не одно поколение ученых и способствуют созданию новых отраслей биологической науки. Выбор приоритетных направлений, способствующих скорейшей реализации поставленной задачи, затруднен установлением критериев оценки значимости их дальнейшего развития, что предопределено как объективными, так и субъективными причинами. Исследователь на различных этапах своей деятельности сталкивается с наличием не только противоположных мнений, но даже направлений работы, которые, в свою очередь, могут, как исключать, так и дополнять друг друга. Ошибка выбора приоритета развития как раз и заключается в выделении какой-либо из особенностей, отрицая остальные и, забывая принцип соотношения Бора о том, что каждая новая теория должна включать в себя элемент старой как предельный случай новой. Даже противоположные направления зачастую имеют общее, объединяющее начало не только при выборе объекта исследования или методологии, а и при постановке задачи в целом. Важно отыскать это начало и попытаться оттолкнуться от него.

Создание алгоритма объективной оценки изучаемого явления с учетом всего спектра составляющих его качеств позволяет получить максимальный эффект при его дальнейшей реализации.

Выполнение эксперимента (см. структурную схему проведения биологического исследования) сопряжено с проведением измерений и их статистической обработкой, начиная от поисковых опытов и кончая выполнением всего эксперимента в целом. По окончанию статистической обработки эксперимента можно приступать к обобщению экспериментальных данных.

Вопросы для самоконтроля.

1 При каких условиях осуществляется равноточность измерения?

2 Назовите критерий оценки равноточности измерения.

3 Какова необходимость вычисления средней взвешенной величины и ее ошибки?

4 Как производится сравнение средних значений для определения существенности различия между двумя вариационными рядами?

5 Перечислите основные функции нормированного отклонения.