Знаходження оптимального розміру партії поставки з урахуванням можливого дефіциту запасів
Відміна даної моделі управління запасами від попередньої полягає в тому, що на відміну від моделі Уілсона ми допускаємо можливість дефіциту запасу на протязі деякої частки інтервала постави. Вважається, що заявки, які надійшли на склад в той момент, коли на ньому відсутні запаси не втрачаються, а заборговуються (заборгованй попит), тобто стають першими в чергу на виконання і задовільняються першочергово після надходження партії товару на склад. За час заборгування (час простою незадовільненої заявки) склад несе відповідальність у вигляді або штрафних санкцій, або задовільняє заборговані заявки з дисконтом; розмір санкцій пропорційний часу простоя.
В цьому випадку графік динаміки зміни рівня запасу на складі має вигляд, який наведено на рис. 2.
Відомо, що в цьому випадку сукупні витрати управління запасами складають
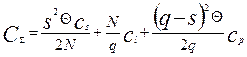 , (5)
, (5)
де де N – сукупний прогнозуємий попит за плановий період; Θ – плановий період (горизонт планування); q – розмір партії поставки; cl; - вартість організації поставки однієї партії cs – приведена вартість зберігання одиниці запасу в одиницю часу; s – максимальний рівень запасу на складі; cp – вартість збитків складу від відсутності одиниці запасу в одиницю часу.
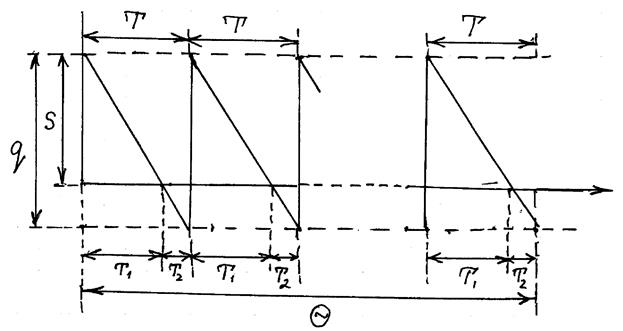
Рис. 2. Динаміка руху запасів при наявності дефіциту
В формулі (5) у нас дві керовані кількістні змінні – максимальний рівень запасів на складі і розмір партії поставки. Взявши похідні витрат (5) по цим змінним, прирівнявши їх до нуля і розв’язавши рівняння, отримаємо, що оптимальні значення цих параметрів, які мінімізують сукупні витрати управління запасами, дорівнюють
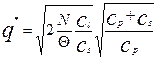 , (6)
, (6)
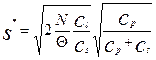 , (7)
, (7)
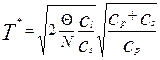 . (8)
. (8)
З геометричних побудов рис. 8.2 видно, що

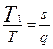 і
і 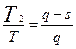 . (9)
. (9)
Підставивши оптималльні значення параметрів політики управління запасами (6) – (8) в пропорції (9), можна точно обрахувати періоди бездефіцитності на складі і інтервал часу, в якому дефіцт допускається. В цьому випадку витрати управління запасами складуть мінімальрого значення, яке буде дорівнювати
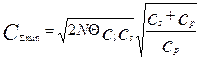 . (10)
. (10)
Порівнявши формули (4) і (10) можна зробити висновок, що витрати управління запасами при наявності дефіциту завжди менше ніж без нього (другий радикал у формулі (10) меньше одиниці) навіть при сплаті штрафів за заборгований попит. Отже фірма може знижати операційні логістичні витрати зп рахунок свідомого створення штучного дефіциту на певний інтервал часу Т2 Як показують дослідження, економія в залежності від значень параметрів моделі може досягти 12%. Ясно, цю модель можна застосовувати тільки в випадках, коли дефіцит не призведе до втрати клієнта (або корпоративні клієнти, або гнучка приваблива система штрафів і скидок по ціні), тобто попит на протязі всього горизонту планування змінюватися не буде.
Дата добавления: 2016-07-22; просмотров: 1795;











