Алгоритмы оптимального резервирования

При решении задач оптимального резервирования используются различные методы оптимизации. Рассмотрим некоторые из этих методов.

Градиентный метод.

В общем случае решение задачи градиентным методом заключается в том, что отыскивается значение экстремума некоторой функции путём последовательных шагов из начальной точки по направлению градиента целевой функции. При этом для решения задачи требуется лишь знание функции и ё первых частных производных в момент начала каждого очередного шага.

Процесс создания оптимальной резервированной системы этим методом представим в виде следующего многошагового процесса. Вначале рассматривается исходная нерезервированная система и на первом шаге отыскивается элемент системы (подсистема) добавление к которой одного резервного элемента даёт наибольший удельный выигрыш в приросте показателя надёжности системы в целом, т.е. надёжности системы к приросту затрат. На втором шаге отыскивается следующий элемент системы (подсистема), (включая и тот, у которого уже есть резервный элемент), который характеризуется наибольшим удельным выигрышем в приросте показателя надёжности и т.д. Допустим, что на некотором N-ом шаге построенного таким образом процесса каждая i-ая подсистема уже имеет 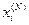резервных элементов: .

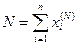Функция надёжности системы на N-ом шаге процесса: .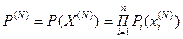

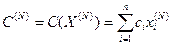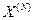Затраты на обеспечение этой надёжности: , где - вектор состава резервных элементов на N-ом шаге.

В соответствии с описанной процедурой на следующем “N+1”-ом шаге процесса отыскивается максимальное значение из всех рассчитываемых по формуле (11.3) для каждой подсистемы.

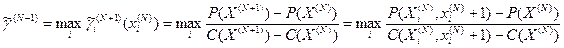(11.3), где 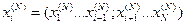, 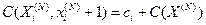и далее .

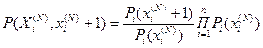Тогда 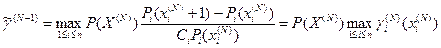, где 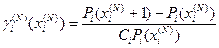. Отсюда видно, что содержание процесса движения к экстремуму не изменится, если на “N+1”-ом шаге мы будем двигаться в направлении 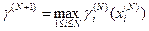. Таким образом, рассчитав для каждого участка значение 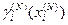можно определить в какой последовательности следует добавлять резервные элементы, чтобы остановившись на любом произвольном шаге процесса мы имели бы систему, резерв которой оптимален в рассматриваемом смысле.

Для высоконадёжных систем 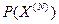и 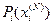близки к единице, поэтому можно записать приближенное выражение:

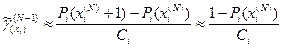
Процесс прекращается на таком шаге N, когда для прямой задачи 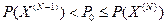. Для обратной задачи: .

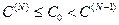Градиентный метод не даёт строгого оптимального решения, т.е. перебор ведётся в ограниченной области возможных решений. Из любой точки процесса решения, характеризуемой некоторым вектором состава системы X^(N) можно прийти только в такую точку “N+1”, чтобы выполнилось условие X^(N+1)>X^(N). Иначе говоря, после каждого шага в системе обязательно добавляется резервный элемент. Перекомпоновка резерва между подсистемами не допускается. Метод может быть рекомендован на этапах предварительного проектирования надёжных систем.

Пример решения задачи оптимального резервирования градиентным методом рассмотрен в [20,21].