Алгоритм оптимального приёма при полностью известных сигналах. Когерентный приём

Полностью известными называются сигналы, у которых известны информационные параметры (то есть параметры, которые модулируются).

Когерентный приём – это приём полностью известных сигналов.

Предположим, что в канале действует наиболее типичная помеха – гауссовский аддитивный шум N(t), который в начале будем считать белым (широкополосным) со спектральной плотностью 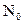. Это значит, что при передаче сигнала 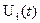(символа 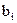, i=0,1, …,m-1) приходящий сигнал можно описать моделью:

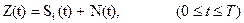(3.11)

где все 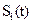известны. Неизвестны лишь реализация помехи и индекс i действительно переданного сигнала, который и должна определить решающая схема.

Будем так же считать, что все сигналы 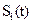являются финитными.

Определим в этих условиях алгоритм работы оптимального приёмника, анализирующего сигнал на тактовом интервале 0-Т по критерию максимального правдоподобия.

Алгоритм предусматривает ряд отдельных последовательных действий – «шагов»

1) Примем так называемую нулевую (или шумовую) гипотезу: S(t)=0; Z(t)=N(t)

То есть предположим, что на вход приёмника поступает только шум.

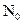2) Задача затрудняется тем, что ширина спектра сигнала бесконечна (поскольку он финитный), а поэтому пространство сигналов бесконечное. Для таких сигналов не существует плотности вероятностей. Однако существуют n-мерные плотности вероятностей для любых n сечений сигнала. Поэтому заменим белый шум квазибелым, имеющим ту же одностороннюю спектральную плотность мощности , но только в некоторой полосе частот F.

3) Возьмём на тактовом интервале (Т) n равноотстоящих сечений через 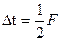. Отсчёты 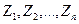в этих сечениях квазибелого гауссовского шума независимы.

4) Поэтому n-мерная плотность вероятностей для взятых отсчётов:

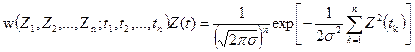(3.12)

где 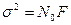– дисперсия (мощность) квазибелого шума.

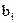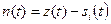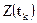
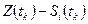5) При гипотезе, что передавался символ , согласно (3.11) . Следовательно, условная n-мерная плотность вероятности сечений Z(t) определяется такой же формулой, как и (3.12), если заменить разностью , представляющей при этой гипотезе шум:

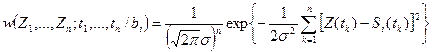(3.13)

6) Отношение правдоподобия для сигнала 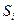(относительно дополнительной гипотезы), вычисленное для n сечений:

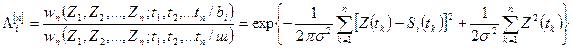
(3.14)

7) Заменим дисперсию 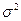её выражением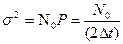

Тогда

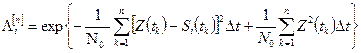(3.15)

8) По правилу максимума правдоподобия в случае квазибелого шума решающая схема должна выбирать значение i, обеспечивающее максимум 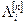. Вместо максимума 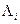можно отыскивать максимум его логарифма:

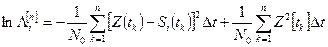(3.16)

9) Второй член в (3.16) можно при сравнении гипотез не учитывать, он сокращается. Тогда правило решения о том, что передавался символ 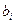, согласно (3.7) можно выразить системой неравенств:

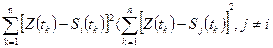(3.17)

10) Вернёмся теперь к исходной задаче для белого шума. Для этого будем расширять полосу F, тогда число сечений n стремится к бесконечности, 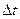– к нулю. Суммы в (3.17) обратятся в интегралы, и правило решения определяется так:

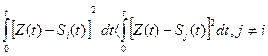(3.18)

Выражение (3.18) определяет те операции (алгоритм работы), которые должен совершать оптимальный приёмник над входным колебанием Z(t).