Система масового обслуговування М/М/1

Ця СМО являє собою одноканальну (з одним приладом) систему масового обслуговування з необмеженою чергою. Процедура обслуговування – безпріоритетна FIFO. На вхід у систему поступає пуасонівський потік клієнтів з інтенсивністю 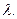Час обслуговування клієнтів є незалежними випадковими величинами, розподіленими по експоненційному закону із середнім значенням 1/ 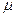. Рівняння Чепмена-Колмогорова для такої СМО мають вигляд

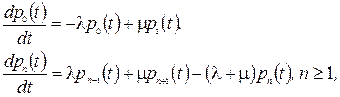
де 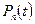імовірність того, що в довільний момент часу t в СМО буде рівно N клієнтів.

Умовно стаціонарного режиму роботи СМО буде

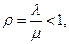
де 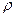– завантаження (коефіцієнт використання) системи.

В стаціонарному режимі 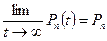і розподіл ймовірностей має вигляд

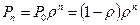
Використовуючи властивості математичних очікувань знайдемо числові характеристики систем М/М/1:

- середня кількість клієнтів у системі

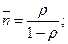
- середня кількість у черзі

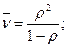
- середній час перебування клієнта в СМО

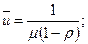
- середній час перебування клієнта в черзі

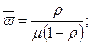
- формули Літла

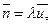
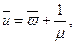
Додаток 2

Метод невизначених множників Лагранжа

Метод невизначених множників Лагранжа є основним методом розв’язку задач умовної оптимізації, коли цільова функція і обмеження не є лінійними функціями. Сутність методу полягає в наступному.

Припустимо, нам потрібно знайти екстремум функції n змінних 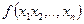. На цю функцію накладаються m обмежень, виду 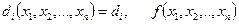співпадає з екстремумом функції Лагранжа

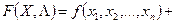
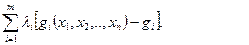(д.1)

В самому ділі, оскільки квадратна дужка в (д. 1) дорівнює нулю, то функція фактично не змінилась. Але тепер кількість змінних збільшилась до n+m, n – кількість змінних в задачі, m – кількість обмежень, які введені у функцію Лагранжа за рахунок m множників Лагранжа 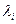, значення яких нам невідомо.

Розв’язком задачі пошуку екстремуму (д. 1) буде розв’язок системи