Математичні моделі оптимізації пропускних спроможностей і потоків на мережах

Загальні положення

В даному розділі розглядаються задачі оптимізації пропускних спроможностей і потоків на мережах, які функціонують під впливом випадкових факторів. В цих задачах вважається, що відома топологія мережі (як правило, транспортної або виробничої). Ця мережа складається з М дуг (каналів, шляхів виробничих ланок) і N вершин (вузлів, пунктів розвантаження товарів, складів). Вважається, що канали є абсолютно надійними, а пропускна спроможність і-го каналу дорівнює 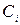(одиниць потоку/одиницю часу). Матеріальний потік, який поступає на мережу є випадковим процесом, розподіленим по куасоновському закону із середнім значенням 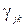(одиниць потоку/одиницю часу) для тих елементів потоку, які виникають в вузлі 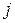і призначені для вузла 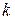. Повний потік який поступає в мережу і залишає її дорівнює

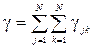(3.1)

час обслуговування потоку в каналах є випадкова величина, розподілений по експоненційному закону із середнім значенням 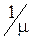(залежить від параметрів товару або операції, величини партії і т.ін.). тоді кожен канал (дуга) мережі являє собою систему масового обслуговування (СМО) типу М/М/1 (див. Додаток 1).

Оскільки кожний канал в мережі розглядається як окремий прибор обслуговування, позначимо через 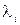середнє число елементів потоку (інтенсивність потоку), яке проходить по і-му каналу в одиницю часу. Тоді повний графік в мережі дорівнює

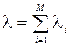(3.2)

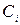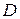Припустимо, що вартість побудови (впровадження) і-го каналу з пропускною спроможністю задається деякою довільною функцією . Позначимо через вартість всієї мережі, тоді

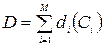(3.3)

Позначимо через Т повний час, який елемент потоку проводить в мережі. В зв’язку з тим, що кожен канал є СМО М/М/1, мова може йти про середнє значення цього часу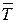

.

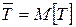Якщо позначити через 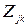середній час проходження по маршруту 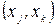, то можна записати

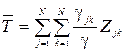, (3.4)

Тому що частка 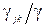повного потоку має в середньому затримку 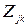. Рівність (3.4) є фактично розкладом мережі по парам джерело-адресат.

Отже, при такому підході транспортна логістична система є мережею масового обслуговування Джексона.

В цьому випадку можливі три постановки задачі:

1) вибір пропускних спроможностей каналів ;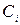

2) вибір потоків в калах ;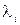

3) розробка топології мережі.

Оскільки ми вважаємо, що топологія мережі задана, розглянемо перші дві постановки.

В залежності від того, що вважати критерієм ефективності, а що – обмеженнями (залежить від конкретної виробничої ситуації) можливі чотири оптимізаційні задачі.

Задача вибору пропускних спроможностей.

Дано: потоки 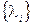і топологія мережі.

Мінімізувати: Т

Варіюються: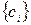

Обмеження: .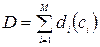

Задача розподілу потоків.

Дано: пропускні спроможності 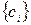і топологія мережі.

Мінімізувати: Т

Варіюються: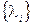

Обмеження: .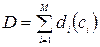

Задача вибору пропускних спроможностей.

Дано: потоки 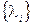і топологія мережі.

Мінімізувати: D

Варіюються: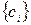

Обмеження: 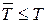критичне.

Задача розподілу потоків.

Дано: пропускні спроможності 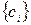і топологія мережі.

Мінімізувати: D

Варіюються: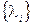

Обмеження: 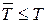критичне.

Можливі також комбіновані постановки задач оптимізації, наприклад, задача вибору пропускних спроможностей і розподілу потоків при обмеженні на сумарну вартість коштів проекту.

З аналізу наведених задач ясно, що всі вони є задачами умовної оптимізації з обмеженнями. В зв’язку з тим, що обмеження і цільова функція є нелінійними, стандартними засобами розв’язку таких задач є метод невизначених множників Лагранжа. Коротку сутність цього методу наведено в Додатку 2.

Зробимо ще одне коротке зауваження перед тим, як перейдемо до розгляду задач оптимізації відмітимо, що якщо задач не має обмежень, то вона розв’язується по алгоритму Форда-Фалкерсона, який наведено в попередньому розділ.