Задача вибору пропускних спроможностей

Однією з найбільш важливих і тяжких задач проектування транспортної мережі є оптимальний вибір пропускних спроможностей каналів мережі з скінченого набору їх можливих значень. Не дивлячись на те, що існує багато евристичних підходів до розв’язку цієї задачі, є нестача в її точних аналітичних розв’язках.

Для того, щоб вивчити теоретичні властивості оптимального набору пропускних спроможностей, будемо вважати, що пропускні спроможності можуть приймати неперервні значення, хоча на практиці це дискретна величина. Зауважимо, що відношення 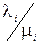– є середнє число одиниць потоку, яке проходить по і-му каналу і тоді потрібно зробити такий вибір, щоб для кожного каналу виконувалось співвідношення .

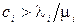Почнемо з розгляду лінійних вартісних функцій пропускних спроможностей. Тоді маємо

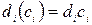(3.5)

Коефіцієнт 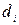є вартість в розрахунку на одиницю пропускної спроможності каналу. Цей коефіцієнт може довільно змінюватись в залежності від будь-якого параметру (технічного) каналу, але він повинен лінійно залежати від пропускної спроможності. На практиці звичайно 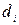береться пропорційно довжині каналу.

Тоді ставиться задача мінімізувати середній час перебування матеріального потоку в мережі 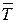(3.4) при обмеженні на сумарний капітал 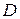(3.3), який вкладається в створення мережі. Для мінімізації 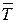складемо функцію Лагранжа

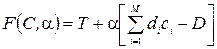, (3.6)

де с – вектор пропускних спроможностей каналів;

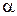– множник Лагранжа.

Так як кожен канал є системою масового обслуговування М/М/1, то 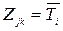є середнім часом перебування одиниць потоку в і-й СМО, а 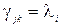– інтенсивність вхідного потоку в цю СМО. Тоді функція (3.6) прийме вигляд

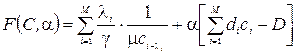. (3.7).

Візьмемо М похідних 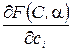, тоді отримаємо М рівня виду

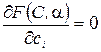, і=1,2,..., М.

Це дає

,

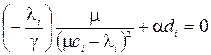або

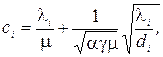і=1,2,..., М. (3.8)

В рівнянні (3.8) нам невідома величина множника Лагранжа 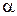. Для його визначення підставимо розв’язки (3.8) в обмеження (3.5), де D – величина капіталу, що вкладається в мережу. Маємо

.

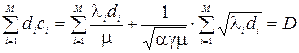Тоді

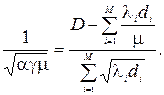(3.9)

Позначимо

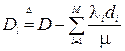(3.10)

Підставивши (3.9) і (3.10) в (3.8), отримає нарешті значення

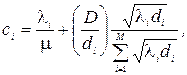i = 1, 2, ..., М (3.11)

При такому наборі пропускних спроможностей час затримки елементів потоку в мережі буде мінімальною, а витрачені кошти не перевищать заданої величини D.

Якщо підставити (3.11) в (3.4), отримаємо, що мінімальне значення цього часу складає

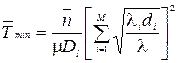, (3.12)

де 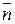середнє значення одиниць потоку в мережі.

Зауваження. З (3.12) видно, що при 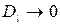значення 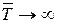. Це означає, що потік перевищує мінімальний розріз мережі, задача розв’язку не мав, а отже потрібно збільшувати обсяг капітальних вкладень D.