Алгоритм: задача построения минимального каркаса.

Деревья.

Деревом называется конечный связный неориентированный граф, имеющий не менее двух вершин и не содержащий циклов (петель и кратных рёбер).

Лесом называется граф без циклов связной компоненты которого являются деревья.

Теорема 1: Если граф G(x) имеет n вершин (n>1), то следующие характеристики свойства деревьев равносильны:

1) G(x) связен, нет циклов.

2) G(x) связен, не содержит циклов и имеет n-1 рёбер.

3) G(x) связен и имеет n-1 рёбер.

4) G(x) не содержит циклов, но добавление ребра между двумя любыми несмежными вершинами приводит к появлению одного элементарного цикла.

5) G(x) связен, но утрачивает свойства после удаления ребра.

6) Всякая пара вершин связна цепью, притом одной.

Любое из этих свойств можно рассмотреть как определение дерева.

Теорема 2: Граф G(x) ó содержит частичный граф и является деревом, когда он связен.
Доказательство:

1) Необходимость. Предположим, что граф G(x) не связен, поэтому его частичные графы не связны, так как частичный граф строится на том же множестве вершин.

2) Достаточность. Предположим, что граф G(x) связен, проверим нет ли у него такого ребра, удаление которого нарушит связность. Согласно теореме 1 сам граф G(x) будет деревом, если таких рёбер нет. Если такое ребро есть, то удалим его и проверим, нет ли подобных рёбер в оставшемся частном графе и так далее. Очевидно, что через конечное число шагов мы получим граф без таких рёбер, то есть получим дерево.

3) Резюме. Доказательство теоремы даёт алгоритм построения в заданном графе частного, то есть дерева, его назовём частичным графом, покрывающим деревом, каркасом для связного графа.

Пример:

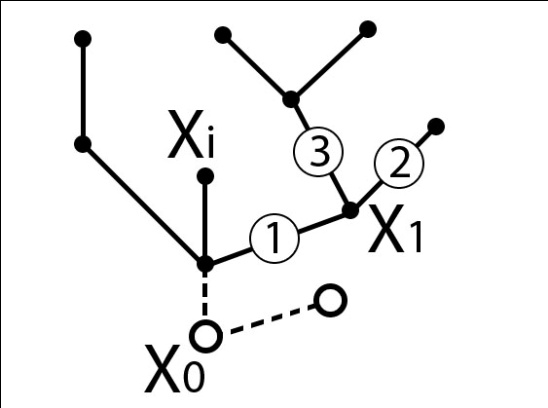Пусть задано множество вершин, на котором нужно построить дерево из оставшихся вершин х_i . Проведём рёбра на расстоянии ① от вершины х₀ , затем ②, ③ и так далее. Вершину х₀ назовём корнем дерева. Не существует ни одного ребра (x’_n_-1 , x”_n_-1), так как появился бы цикл и граф не был бы деревом. Иногда в графе выгодно выделить какую-то цепь, которая называется стволом дерева. Любая вершина, лежащая на стволе, связана со стволом элементарной цепью – ветвь дерева.

Вопрос: Сколько различных деревьев можно построить на n – пронумерованных вершинах.

Решена Кели, показав, что на n – пронумерованных вершинах можно построить nⁿ^-2 , результат Кели позволяет сделать следующий вывод:

Имеется n городов, сколькими способами можно построить дороги между ними, чтобы путник мог спокойно их обойти, не останавливаясь в поисках пути и не возвращаясь назад.

Пусть также известно стоимость дорог µ( x_i , x_j ). Какие именно линии можно построить, чтобы все города были связаны, а стоимость минимальна.

Алгоритм: задача построения минимального каркаса.

1) В графе G(x) выбирается ребро, имеющее наименьшую меру. Ребро Е₁ , то есть это ребро образец частичного подграфа графа

G(x) А₁ (Е₁ 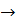А₁).

Рассмотрим первый шаг. На этом шаге к уже построенному частному графу А_i_-1 добавляем ребро Е_i , имеющее минимальную меру среди всех неисследованных рёбер.

Ограничение: добавление ребра Е_i к А_i_-1 не должно приводить к образованию цикла, иначе нужно брать другое ребро. Если имеется несколько рёбер с одинаковыми мерами и удовлетворяющими данному условию, то можно выбирать любое из них.

В соответствии с теоремой 1, на n-1 шаге мы построим частный подграф А_n_-1 являющийся каркасом для графа G(x).

Введём доказательство от противного.

Предположим, что покрывающее дерево А_n_-1 не я вляется минимальным каркасом, то есть µ(T) < µ(А_n_-1). Сравним T и А_n_-1 по ходу построения. Пусть Е_i первое по ходу построения ребро графа Е_i , которое не принадлежит дереву Т, присоединим это ребро к дереву Т, в результате получим объединенный граф Т 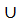Е_i . По построению граф А_n_-1 также является деревом и не содержит циклов, соответственно в этом цикле должно быть хотя бы одно ребро Е’ не принадлежащее

А_n_-1.

Отвергнуть Е’ мы не можем, так как он принадлежит Т. Удали ребро Е’ из графа А_n_-1 , получим граф Т₁ = (Т 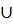Е_i)\Е’. После удаления ребра граф разрушится, но оставшийся граф Т₁ – покрывающий, с каркасом определяющим меру µ(T₁). Наверняка µ(T₁) 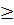µ(T), так как это минимальная мера.

2) Рассмотрим меру µ(Е_i) 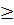µ(Е’). ②

Рассмотрим в этом неравенстве случай с равенством µ(Е_i) 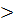µ(Е’). Если бы в графе была мера Е_i 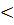Е₁ , то возвращаемся на шаг 1 и выполняем соответствующие действие. Фактически имеет место равенство

µ(Е_i) = µ(Е’), соответсвенно мерой графа µ(Т₁) = µ(Т) и получим минимальное значение графа, аналогичная операция производится с графами А_n_-1 и Т₁ , то есть получим решение:

Т₂ = (Т₁ 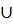Е_j)\Е”, через конечное число шагов получим каркас совпадающий с А_n_-1 , являющийся минимальной мерой, то есть Т и есть минимальный каркас.

Циклический ранг

Циклический ранг (цикломатическое число) – замечательные числа графа.

Пусть G(x) конечный, связный неориентированный граф. Построим граф из его рёбер. Берём произвольное ребро, далее добавляем к данной части любое ребро, соединённое с ней хотя бы одной общей вершиной. На каждом шаге будем вычислять цикломатическое число.

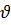_i = m_i – n_i + 1 (где m_i – число использованных рёбер, n_i – вершины).

1: m₁ = 1, n₁ = 2 => ₁ = 0.

Если на каждом шаге число 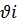не уменьшается, а увеличивается на единицу, то 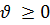, если граф 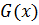имеет m рёбер и n вершин, то 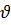_n = 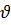(G) = m – n +1 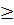0 – это число называется цикломатическим числом графа.

12 3 4

Дата добавления: 2016-06-05; просмотров: 3095;